25 братаны, кто разбирается в этом чертовом предмете? 1. укажите верное утверждение: 1) квадратное уравнение, у которого коэффициент а=1, называется . 2) квадратное уравнение, у которого коэффициент а=1, называется . 3) квадратное уравнение, у которого коэффициент а=1, называется неполным. 2. какие из чисел являются корнями уравнения 2х2 + 5х – 3 = 0. 1) 3; 0,5 2) –0,5; -3 3) 0,5; -3 4) 1; 0 3. найдите дискриминант квадратного уравнения х2 – 6х + 9 = 0. 1) 2 2) 9 3) 0 4) 36 4. найдите наибольший корень уравнения 5х2 – 7х + 2 = 0. 1) 0,4 2) 1 3) –1 4) 2 5. при каких значениях m можно представить в виде квадрата двучлена выражение х2 – 2х – m. ответ: 6. решите уравнение 7х = 4 х2. 1) 0; - 1,75 2)1,4; 1,75 3) –3; 0 4) 0; 1,75 7. найдите сумму корней уравнения : 7х2 + 6х – 1 = 0. 1) 2) 1 3) – 0,5 4) –1 8. установите соответствие между данными уравнениями и знаками их корней: 1) -3х2 + 6х + 1 = 0 а) оба корня положительны 2) -х2 + 10х – 11 = 0 в) оба корня отрицательны 3) 5х2 + 17х + 5 = 0 с) корни разных знаков 9. один из корней квадратного уравнения 5х2 – 7х + k = 0 равен -2 .найдите k. 1) – 47,6 2) –53 3) 54 4) 30 10. найдите произведение корней уравнения: (5 + 4х)2 = (9 – 21х)(4х + 5). 1) 2 2) – 0,2 3) 0,2 4) нет решений
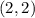
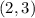
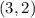
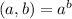 - где a-число оценок, b-число учеников.
- где a-число оценок, b-число учеников.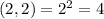
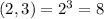
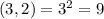
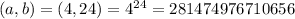
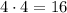 - варианта событий.
- варианта событий.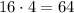 - варианта событий.
- варианта событий.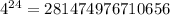 - вариантов событий.
- вариантов событий.
2 - 3
3 - 3
4 - 2
5 - (-1)
6 - 4
7 - (-6/7)
8 - 1-с
2-а
3-в
9 -
10 - 2