Выражения использую свойства степени с целым показателем .(номер 7.1 ) и представить выражения в виде степени с цел.показ. (номер 7.2)

👇

Увидеть ответ

Ответ:

Amina0807

12.05.2020

решение во вложении:

Выражения использую свойства степени с целым показателем .(номер 7.1 ) и представить выражения в вид

4,4(66 оценок)

Ответ:

dalilkadyrkulov

12.05.2020

ответ и решение во вложении

4,5(76 оценок)

Открыть все ответы

Ответ:

alexandra977

12.05.2020

В треугольнике : α+β+γ=π ⇒ γ=π-α-β=π-(α+β)

tgα/2*tgβ/2+tgβ/2*tgγ/2+tgγ/2*tgα/2=

=tgα/2*tgβ/2+tgβ/2*tg(π/2-(α+β)/2)+tg(π/2-(α+β)/2)*tgα/2=

=[ tg(π/2-a)=ctga по формулам приведения]=

=tgα/2*tgβ/2+ctg(α+β)/2 * (tgβ/2+tgα/2) = [формула tga+tgb=sin(a+b)/cosacosb ] =

sinα/2 * sinβ/2 α+β sin(α+β)/2 sinα/2 * sinβ/2 cos(α+β)/2

= + ctg * = + *

cosα/2 * cosβ/2 2 cosβ/2 * cosα/2 cosα/2 * cosβ/2 sin(α+β)/2

sin(α+β)/2 1/2[cos(α-β)/2-cos(α+β)/2] + cos(α+β)/2 1/2(cos(α-β)/2+cos(α+β)/2)

* == =

cosα/2 *cosβ/2 cosα/2 * cosβ/2 cosα/2 * cosβ/2

1/2 * 2 * (cosα/2 * cosβ/2)

= = 1

cosα/2 * cosβ/2

4,5(65 оценок)

Ответ:

тобик55555555

12.05.2020

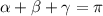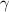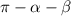Так как сумма углов в треугольнике равна $\alpha+\beta+\gamma=\pi$ , то вместо $\gamma$ запишем $\pi-\alpha-\beta$ .

Тогда

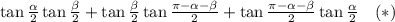
$\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\tan\frac{\beta}{2}\tan\frac{\pi-\alpha-\beta}{2}+\tan\frac{\pi-\alpha-\beta}{2}\tan\frac{\alpha}{2}\quad (*)$

Вычислим отдельно тангенс.

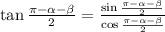
$\tan\frac{\pi-\alpha-\beta}{2}=\frac{\sin\frac{\pi-\alpha-\beta}{2}}{\cos\frac{\pi-\alpha-\beta}{2}}$

Вычислим отдельно числитель и знаменатель

Числитель равен

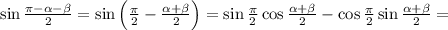
$\sin\frac{\pi-\alpha-\beta}{2}=\sin\left(\frac{\pi}{2}-\frac{\alpha+\beta}{2}\right)=\sin\frac{\pi}{2}\cos\frac{\alpha+\beta}{2}-\cos\frac{\pi}{2}\sin\frac{\alpha+\beta}{2}=$

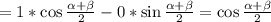
$=1*\cos\frac{\alpha+\beta}{2}-0*\sin\frac{\alpha+\beta}{2}=\cos\frac{\alpha+\beta}{2}$

Знаменатель равен

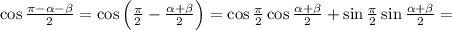
$\cos\frac{\pi-\alpha-\beta}{2}=\cos\left(\frac{\pi}{2}-\frac{\alpha+\beta}{2}\right)=\cos\frac{\pi}{2}\cos\frac{\alpha+\beta}{2}+\sin\frac{\pi}{2}\sin\frac{\alpha+\beta}{2}=$

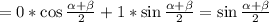
$=0*\cos\frac{\alpha+\beta}{2}+1*\sin\frac{\alpha+\beta}{2}=\sin\frac{\alpha+\beta}{2}$

Значит

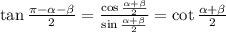
$\tan\frac{\pi-\alpha-\beta}{2}=\frac{\cos\frac{\alpha+\beta}{2}}{\sin\frac{\alpha+\beta}{2}}=\cot\frac{\alpha+\beta}{2}$

Подставим в исходную формулу (*)

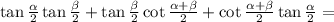
$\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\tan\frac{\beta}{2}\cot\frac{\alpha+\beta}{2}+\cot\frac{\alpha+\beta}{2}\tan\frac{\alpha}{2}=$

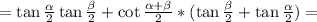
$=\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\cot\frac{\alpha+\beta}{2}*(\tan\frac{\beta}{2}+\tan\frac{\alpha}{2})=$

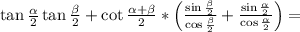
$\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\cot\frac{\alpha+\beta}{2}*\left(\frac{\sin\frac{\beta}{2}}{\cos\frac{\beta}{2}}+\frac{\sin\frac{\alpha}{2}}{\cos\frac{\alpha}{2}}\right)=$

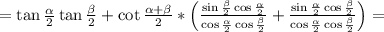
$=\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\cot\frac{\alpha+\beta}{2}*\left(\frac{\sin\frac{\beta}{2}\cos\frac{\alpha}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}+\frac{\sin\frac{\alpha}{2}\cos\frac{\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}\right)=$

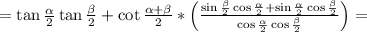
$=\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\cot\frac{\alpha+\beta}{2}*\left(\frac{\sin\frac{\beta}{2}\cos\frac{\alpha}{2}+\sin\frac{\alpha}{2}\cos\frac{\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}\right)=$

По формуле синуса суммы

sin(x+y)=sinx*cosy+sinycosx

преобразуем числитель в скобках

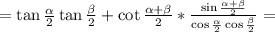
$=\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\cot\frac{\alpha+\beta}{2}*\frac{\sin\frac{\alpha+\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}=$

Снова распишем котангенс по определению

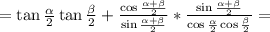
$=\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\frac{\cos\frac{\alpha+\beta}{2}}{\sin\frac{\alpha+\beta}{2}}*\frac{\sin\frac{\alpha+\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}=$

Проведем сокращения

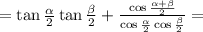
$=\tan\frac{\alpha}{2}\tan\frac{\beta}{2}+\frac{\cos\frac{\alpha+\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}=$

По формуле

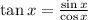$\tan x=\frac{\sin x}{\cos x}$ преобразуем выражение далее

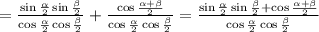
$=\frac{\sin\frac{\alpha}{2}\sin\frac{\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}+\frac{\cos\frac{\alpha+\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}=\frac{\sin\frac{\alpha}{2}\sin\frac{\beta}{2}+\cos\frac{\alpha+\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}$

Распишем в числителе косинус суммы по формуле

cos(x+y)=cosxcosy-sinxsiny

После несложных преобразований и сокращения, получим нужное

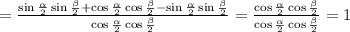
$=\frac{\sin\frac{\alpha}{2}\sin\frac{\beta}{2}+\cos\frac{\alpha}{2}\cos\frac{\beta}{2}-\sin\frac{\alpha}{2}\sin\frac{\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}=\frac{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}{\cos\frac{\alpha}{2}\cos\frac{\beta}{2}}=1$