√f(x) ≥ g(x) ⇔ совокупности 2-х систем
1. f(x) ≥ 0
g(x) ≤ 0
2. g(x) > 0
f(x) ≥ g²(x)
√(10 - 7log(2) x + log²(2) x) ≥ 3 - log(2) x
одз x > 0 логарифм
(log(2) x - 2)(log(2) x - 5) > 0 корень
x ∈ (-∞,4] U [32, +∞)
общее x ∈ (0,4] U [32, +∞)
√((log(2) x - 2)(log(2) x - 5)) ≥ 3 - log(2) x
1. f(x) ≥ 0
g(x) ≤ 0
3 - log(2) x ≤ 0
(log(2) x - 2)(log(2) x - 5) ≥ 0
log(2) x = t
t ≥ 3
(t - 2)(t - 5) ≥ 0
[2] [5]
t ≤ 2
log(2) x ≤ 2
x ≤ 4
t ≥ 5
log(2) x ≥ 5
x ≥ 32
x ∈ [32, +∞)
2. g(x) > 0
f(x) ≥ g²(x)
3 - log(2) x > 0
x < 8
10 - 7log(2) x + log²(2) x ≥ (3 - log(2) x)²
10 - 7log(2) x + log²(2) x ≥ 9 - 6log(2) x + log²(2) x
1 ≥ log(2) x
x ≤ 2
учитывая одз
решение x ∈ (0,2] U [32, +∞)
не являются решением натуральные х ∈ (2, 32)
29 чисел от 3 до 31
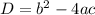(если дискриминант больше нуля уравнение имеет 2 корня, если равен нулю, уравнение имеет 1 корень, если меньше нуля, то нет корней), либо применяя разложение многочлена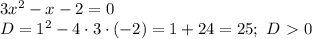
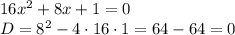
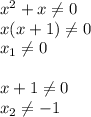
и, поскольку наша прямая проходит через точки (0;0) и (2;3), имеем
х/2=у/3,
у=1,5х.