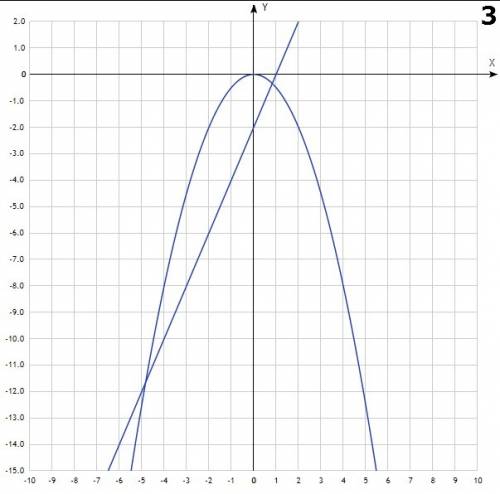
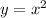При каком значении p вершины парабол y=x^2 - 4px + p и y=-x^2 + 8px + 4 расположены по одну сторону от оси x

👇

Ответ:

05Goryanka05

02.09.2022

Для того, чтобы вершины были расположены по одну сторону от оси абсцисс, ординаты этих вершин должны быть одного знака
Пусть (x1,y1) - вершина y = x^2-4px+p
(x2,y2) - вершина y=-x^2+8px+4
1) y = x^2-4px+p
x1 = 4p / 2 = 2p
y(x1)=4p^2-8p^2+p=-4p^2+p
2) y = -x^2+8px+4
x2 = -8p/-2=4p
y(x2) = -16p^2+32p^2+4=16p^2+4
3) Получим систему
-4p^2+p > 0
16p^2+4 > 0

а) -4p^2+p > 0
p(-4p+1) > 0

p > 0 p<0
-4p+1 > 0 -4p+1<0

p > 0 p<0
p<1/4 p>1/4

0 < p < 1/4 нет решений
б) 16p^2+4 > 0
4(4p^2+1)>0
4p^2+1>0 при x ∈ R
3) общее решение:
0<p<1/4

При всех p, принадлежащих данному промежутку, вершины парабол будут расположены по одну сторону от оси x (в данном случае - выше)
Если нужно конкретное значение, то, например p = 1/8

4,6(52 оценок)

Открыть все ответы

Ответ:

astanina042

02.09.2022

========= 1 =========
График y=x^2

- это парабола, с вершиной в точке (0;0). Она симметрична относительно оси OY. Ветви направлены вверх. Проходит через точки (0;0), (2;4), (-2;4)
График функции y=-2x

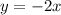- это прямая, для её построения достаточно 2х точек. Например (0;0) и (-2;4)

Точки пересечения: (0;0) и (-2;4)

========= 3 =========

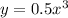График функции y=0.5x^3

- кубическая парабола. График симметричен относительно начала координат, т.е. точки (0;0).
График функции y = 3x +1

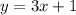- прямая, проходящая через точки (0;1), (1;4)

Приблизительные точки пересечения, исходя из графиков (-0,33; 0,01); (2,6; 8,8); (-2.2;-3,6)

========= 5 =========

График функции y = 2x -2

- прямая, проходящая через точки (0;-2) и (1;0)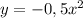
График функции y = -0,5x^2

- парабола, с вершиной в точке (0;0), симметричная относительно OY. Ветви направлены вниз.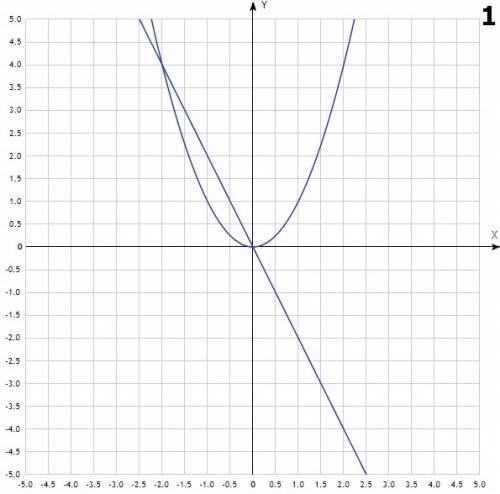

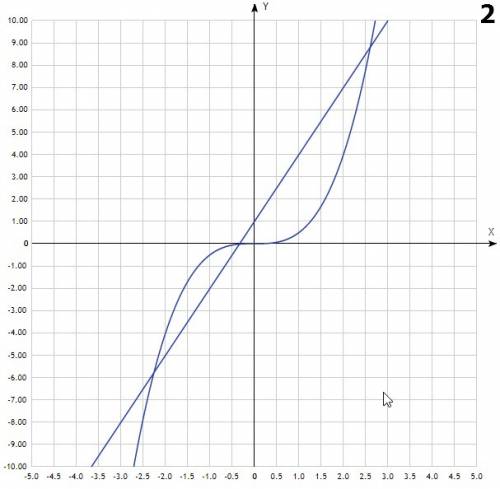
Приблизительные точки пересечения, исходя из графиков (0,81; -0.38) и (-4,9; -11.8)

20 ваши только с на одной координатной плоскости постройте графики функций и найдите (приближенно) к

20 ваши только с на одной координатной плоскости постройте графики функций и найдите (приближенно) к

4,7(65 оценок)

Ответ:

linaaaa2Li

02.09.2022

Объяснение:

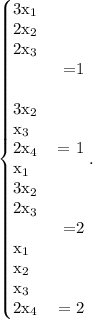
$\left\{\begin{array}{}3x_1&2x_2&2x_3& \ \ \ \ \ \ =1\\&3x_2&x_3&2x_4\ \ =1\\x_1&3x_2&2x_3&\ \ \ \ \ \ \ \ =2\\x_1&x_2&x_3&2x_4\ \ \ =2\end{array}\right..$

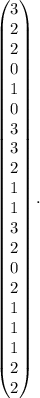
$\left(\begin{array}{}3&2&2&0&1\\0&3&3&2&1\\1&3&2&0&2\\ 1&1&1&2&2\end{array}\right).$

Поменяем местами 1-ю и 3-ю строки:

$\left(\begin{array}{}1&3&2&0&2\\0&3&3&2&1\\3&2&2&0&1\\ 1&1&1&2&2\end{array}\right).$

Вычитаем из 4-й строки 1-ю строку:

$\left(\begin{array}{}1&3&2&0&2\\0&3&3&2&1\\3&2&2&0&1\\ 0&-2&-1&2&0\end{array}\right).$

Вычитаем из 3-й строки 1-ю строку, умноженную на 3:

$\left(\begin{array}{}1&3&2&0&2\\0&3&3&2&1\\0&-7&-4&0&-5\\ 0&-2&-1&2&0\end{array}\right).$

Разделим 2-ю строку на 3:

$\left(\begin{array}{}1&3&2&0&2\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&-7&-4&0&-5\\ 0&-2&-1&2&0\end{array}\right).$

Суммируем 3-ю и 2-ю строку, умноженную на 7:

$\left(\begin{array}{}1&3&2&0&2\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&3&\frac{14}{3} &-\frac{8}{3} \\ 0&-2&-1&2&0\end{array}\right).$

Суммируем 1-ю и 2-ю строку, умноженную на -3:

$\left(\begin{array}{}1&0&-1&-2&1\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&3&\frac{14}{3} &-\frac{8}{3} \\ 0&-2&-1&2&0\end{array}\right).$

Суммируем 4-ю и 2-ю строку, умноженную на 2:

$\left(\begin{array}{}1&0&-1&-2&1\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&3&\frac{14}{3} &-\frac{8}{3} \\ 0&0&1&\frac{10}{3} &\frac{2}{3} \end{array}\right).$

Поменяем местами 4-ю и 3-ю строки:

$\left(\begin{array}{}1&0&-1&-2&1\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&3&\frac{14}{3} &-\frac{8}{3} \end{array}\right).\\$

Суммируем 3-ю и 1-ю строки:

$\left(\begin{array}{}1&0&0&\frac{4}{3} &\frac{5}{3} \\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&3&\frac{14}{3} &-\frac{8}{3} \end{array}\right).\\$

Суммируем 2-ю и 3-ю строку, умноженную на -1:

$\left(\begin{array}{}1&0&0&\frac{4}{3} &\frac{5}{3} \\0&1&0&-\frac{8}{3} &-\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&3&\frac{14}{3} &-\frac{8}{3} \end{array}\right).\\$

Суммируем 4-ю и 3-ю строку, умноженную на -3:

$\left(\begin{array}{}1&0&0&\frac{4}{3} &\frac{5}{3} \\0&1&0&-\frac{8}{3} &-\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&0&-\frac{16}{3} &-\frac{14}{3} \end{array}\right).\\$

Разделим 4-ю строку на -16/3:

$\left(\begin{array}{}1&0&0&\frac{4}{3} &\frac{5}{3} \\0&1&0&-\frac{8}{3} &-\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&0&1 &\frac{7}{8} \end{array}\right).\\$

Суммируем 1-ю и 4-ю строку, умноженную на -4/3:

$\left(\begin{array}{}1&0&0&0 &\frac{1}{2} \\0&1&0&-\frac{8}{3} &-\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&0&1 &\frac{7}{8} \end{array}\right).\\$