В иррациональных уравнениях кроме ОДЗ нужно всегда учитывать дополнительные условия (ДУ) или всегда для проверки подставлять полученные корни в исходное уравнение.
Рассмотрим исходное уравнение: 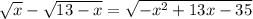
Далее мы возводим это уравнение в квадрат, но это неэквивалентный переход - например, неправильное равенство -1 = 1 переходит в правильное 1 = 1, поэтому на этом этапе легко приобрести лишние корни, что и произошло.
В правой части исходного уравнения находится неотрицательный корень, поэтому в ДУ необходимо потребовать неотрицательность левой части: 
Как раз это ДУ и позволяет в процессе решения откинуть лишний корень 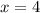
1) ОДЗ: 3 - x ≥ 0 ⇒ x ≤ 3
3-x > 1
-x > - 2
x < 2
ответ: ( - ∞; 2)
2) ОДЗ: ( - ∞; (1-√5) / 2 ] v [ (1+√5) / 2 ; + ∞ )
x² - x -1 ≤ 1
(x+1)(x-2) ≤ 0
Произведение меньше нуля тогда и только тогда, когда оба множителя разных знаков, то есть надо рассмотреть два случая и их объединить:
I случай: x ≤ -1 и x ≥ 2 - решений нет
II случай: x ≥ -1 и x ≤ 2 ⇔ x ∈ [-1; 2]
2 > (1+√5) /2 и -1 < (1-√5) / 2
Тогда с учетом ОДЗ записываем ответ:
ответ: [-1; (1-√5) / 2] v [(1+√5) / 2; 2]
3) ОДЗ: x ∈ ( - ∞; -3] v [3; + ∞ )
(2x-3)² < 4(x²-9)
(2x-3)² - 4(x-3)(x+3) < 0
4x²-12x + 9 - 4x² + 36 < 0
-12x + 45 < 0
x > 3,75
С учетом ОДЗ записываем ответ:
x ∈ ( - ∞; -3 ] v [3,75; + ∞)
x0 = - b/2a = - 0/2*1 = 0
y0 = - 7
(0; - 7)
б)
x0 = - b/2a = - 2/-2 = 1
y0 = - 1^2 + 2*1 = 2 - 1 = 1
(1 ; 1)
в)
x0 = - b/2a = 8/4 = 2
y0 = 2*2^2 - 8*2 + 7 = - 1
(2; - 1)