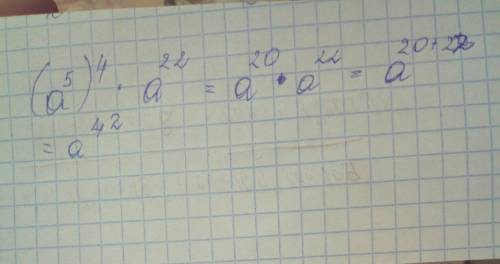
42.
(b+6)(b-6)-b(b+5) при b= -3/5
(b+6)(b-6)-b(b+5)=b²-36-b²-5b=-36-5b
-36-5b=-36-5(-3/5)=-36+3=39
43.
(3-x)²+(4-x)(4+x) при x=5/6
(3-x)²+(4-x)(4+x)=9-6x+x²+16-x²=25-6x
25-6x=25-6•5/6=25-5=20
44.
(2+a)²+(5-a)(5+a) при а=-3/4
(2+a)²+(5-a)(5+a)=4+4а+а²+25-а²=29+4а
29+4а=29+4(-3/4)=29-3=26
45.
(4-с)²+(2-с)(2+с) при с=-3/8
(4-с)²+(2-с)(2+с)=16-8с+с²+4-с²=20-8с
20-8с=20-8(-3/8)=20+3=23
46.
(m+1)²+(6-m)(6+m) при m=1/2
(m+1)²+(6-m)(6+m)=m²+2m+1+36-m²=36+2m
36+2m=36+2•1/2=36+1=37
47.
-m(m+2)+(m+3)(m-3) при m=1/2
-m(m+2)+(m+3)(m-3)=-m²-2m+m²-9=-2m-9
-2m-9=-2•1/2-9=-10
48.
-p(4+p)+(p-2)(p+2) при p=3/4
-p(4+p)+(p-2)(p+2)= -4p-p²+p²-4=-4p-4
-4p-4=-4•3/4-4=-3-4=-7
49.
(n+6)²+(2-n)(2+n) при n=-5/12
(n+6)²+(2-n)(2+n)=n²+12n+36+4-n²=40+12n
40+12n=40+12(-5/12)=40-5=35
В решении.
Объяснение:
Выберите систему уравнений, соответствующую условию задачи: расстояние от поселка до города 62 км;
велосипедист и мотоциклист, выехав одновременно навстречу друг другу, встречаются через час.
Найдите скорость велосипедиста и мотоциклиста, если скорость велосипедиста на 28 км/ч меньше, чем скорость мотоциклиста.
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - скорость велосипедиста.
у - скорость мотоциклиста.
1) х + у = 62
у - х = 28
х = 62 - у
у - 62 + у = 28
2у = 90
у = 45 (км/час) - скорость мотоциклиста.
45 - 28 = 17 (км/час) - скорость велосипедиста.
Второй вариант:
х - скорость мотоциклиста.
у - скорость велосипедиста.
4) х + у = 62
х - у = 28
х = 62 - у
62 - у - у = 28
-2у = 28 - 62
-2у = -34
у = -34/-2
у = 17 (км/час) - скорость велосипедиста.
х = 62 - 17
х = 45 (км/час) - скорость мотоциклиста.
Можно использовать две системы на выбор, в зависимости от обозначений. ответ не изменится.
1) х+у=62
у-х=28
2) х+у=28
х-у=62
3) х+у=28
у-х=62
4) х+у=62
х-у=28