В решении.
Объяснение:
В двух коробках 28 упаковок бумаги. Если из первой коробки переложить во вторую 5 упаковок, то в первой коробке станет в 3 раза меньше упаковок бумаги, чем во второй. Сколько упаковок бумаги во второй коробке?
Решить задачу:
х - в первой коробке сначала.
у - во второй коробке сначала.
По условию задачи система уравнений:
х+у=28
3(х-5)=у+5
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х=28-у
3х-15=у+5
3(28-у)-15=у+5
84-3у-15=у+5
-3у-у=5-69
-4у= -64
у= -64/-4
у=16 (упаковок) - во второй коробке сначала.
х=28-у
х=28-16
х=12 (упаковок) - в первой коробке сначала.
Теперь решить данные в условии уравнения и установить соответствия:
(Б) 3(х-5)=33-х
3х-15=33-х
3х+х=33+15
4х=48
х=48/4
х=12 (по решению задачи известно, что столько упаковок было в первой коробке изначально), условие самое нижнее, третье.
(А) 3(28-х)=х
84-3х=х
-3х-х= -84
-4х= -84
х= -84/-4
х=16 (по решению задачи известно, что столько упаковок было во второй коробке изначально), условие самое верхнее, первое.
(В) 3(23-х)=х+5
69-3х=х+5
-3х-х=5-69
-4х= -64
х= -64/-4
х=16 (по решению задачи известно, что столько упаковок было во второй коробке изначально), условие самое верхнее, первое.
Второму условия нет соответствия среди уравнений. По этому условию х должно быть равно 21 (16+5), такого ответа нет.
В решении.
Объяснение:
1) Сократить дробь:
а) 39х³у/26х²у²=
сократить (разделить) 39 и 26 на 13, х³ и х² на х², у² и у на у:
=3х/2у;
б) 5у/(у²-2у) = 5у/у(у-2) =
сократить (разделить) у и у на у:
= 5/(у-2);
в) (3а-3b)/(a²-b²)=
в числителе вынести 3 за скобки, в знаменателе разность квадратов, развернуть:
=3(a-b)/(a-b)(a+b)=
сократить (разделить) (a-b) и (a-b) на (a-b):
=3/(a+b).
2) Представить в виде дроби:
а) (3-2а)/2а - (1-а²)/а²=
общий знаменатель 2а², надписываем над числителями дополнительные множители:
= [а*(3-2а) - 2*(1-а²)] / 2a²=
=(3а-2а²-2+2а²) / 2a²=
=(3а-2)/2a²;
б) 1/(3х+у) - 1/(3х-у)=
общий знаменатель (3х+у)(3х-у), надписываем над числителями дополнительные множители:
= [(3х-у)*1 - (3х+у)*1] / (3х+у)(3х-у)=
=(3х-у-3х-у) / (3х+у)(3х-у)=
разность квадратов в знаменателе свернуть:
= -2у/(9х²-у²);
в) (4-3в)/(в²-2в) + 3/(в-2)=
= (4-3в)/в(в-2) + 3/(в-2)=
общий знаменатель в(в-2), надписываем над числителями дополнительные множители:
= [1*(4-3в) + в*3] / в(в-2)=
=(4-3в+3в) / в(в-2)=
= 4/в(в-2).
3) Найти значение выражения:
(х-6у²)/2у + 3у= при х= -8; у=0,1
=(х-6у²+6у²)/2у=
=х/2у=
= -8/0,2=
= -40.
4) Упростить:
2/(х-4) - (х+8)/(х²-16) - 1/х= 16/х(х²-16)
=2/(х-4) - (х+8)/(х-4)(х+4) - 1/х=
общий знаменатель х(х-4)(х+4), надписываем над числителями дополнительные множители:
=[х(х+4)*2 - х(х+8) - (х-4)(х+4)*1] / х(х-4)(х+4)=
=(2х²+8х-х²-8х-х²+16) / х(х-4)(х+4)=
разность квадратов в знаменателе свернуть:
= 16/х(х²-16)
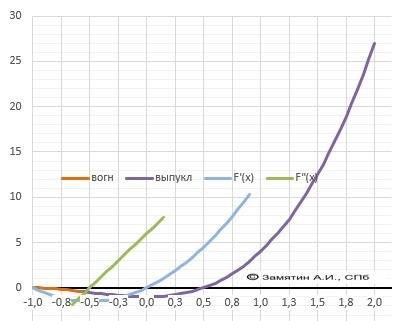
а) промежутки возрастания и убывания функции
f'(x) = 6x² +6x
6x² + 6x = 0
x(6x +6) = 0
x = 0 или 6х +6 = 0
х = -1
-∞ -1 0 +∞
+ - + это знаки 6x² +6x
f(x) возрастает при х∈(-∞; -1)
f(x) убывает при х∈ (-1; 0)
f(x) возрастает при х ∈ (0; + ∞)
б) наибольшее и наименьшее значение функции на отрезке [-1;2]
из найденных критических точек в указанный промежуток попали и -1 и 0
f(-1) = 2*(-1)³ + 3*(-1)² -1 = 0
f(0)= 2*0 +3*0 -1 = -1
f(2) = 2*2³ + 3*2² -1 = 27
max f(x) = f(2) = 27
min f(x) = f(0) = -1
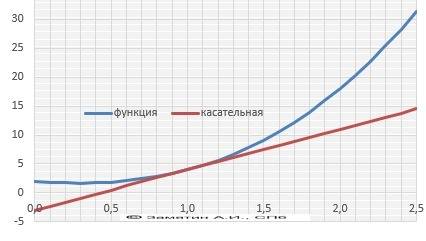
2. Напишите уравнение касательной к графику функции f(x)=x³+3x²-2x+2 в точке с абсциссой x₀=1
y₀ = 1³ +3*1² -2*1 +2 = 4
f'(x) = 3x² +6x -2
f'(1) = 3*1² +6*1 -2 = 7
пишем само уравнение касательной:
у - 4 = 7(х - 1)
у - 4 = 7х -7
у = 7х -3
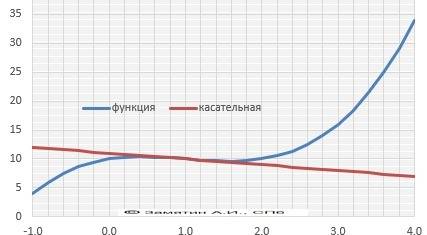
3. Напишите уравнение касательной к графику функции f(x)=x³-3x²+2x+10, параллельной прямой y=-x+5
У прямой у = -х +5 угловой коэффициент = -1. А угловой коэффициент- это производная в точке касания
так что: f'(x) = 3x² -6x +2 = -1, ⇒3x² -6x +3 = 0,⇒ x² -2x +1 = 0, ⇒ x = 1 - это абсцисса точки касания.
х₀ = 1
у₀ = f(1) = 1³ -3*1² +2*1+10 = 10
теперь пишем само уравнение касательной:
у - 10 = -1(х - 1)
у - 10 = -х +1
у = -х +9