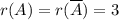По теореме Кронекера-Капелли, система будем совместной тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
При система не совместна. При система совместна, при этом - ранг меньше числа неизвестных, то система имеет бесконечно множество решений. При система совместна, при этом - система имеет единственное решение. При и система совместна, причём система имеет единственное решение, ранг равен числу неизвестных
Так как выражение (7а-3)² нечетное Значит выражение (7а-3) должно заканчиваться цифрами 1, 3, 5, 7, 9. Поэтому 7а должно соответственно заканчиваться 4, 6, 8, 0, 2. А само а заканчивается цифрой 2, 8, 4, 0, 6.
Теперь перебираем все пять вариантов окончания а: а) При а=...2 Получаем а²-1=...3 -нечетное не имеет смысл проверять далее в) При а=...2 Получаем а²+а+1=...7 -нечетное с) При а=...2 Получаем 5а+2=..2 -четное при а=...8 Получаем 5а+2=..2 -четное при а=...4 Получаем 5а+2=..2 -четное при а=...0 Получаем 5а+2=..2 -четное при а=...6 Получаем 5а+2=..2 -четное d) При а=...2 Получаем а³+1=...9 -нечетное е) При а=...2 Получаем 4а-3=...5 -нечетное
Исходное множество состоит из 4 элементов: 1, 2, 3, 4.
Пусть подмножества различимы. Поставим в соответствие разбиению строчку из 4 символов 0 или 1: на i-м месте 0, если число в первом множестве, 1, если во втором.
Понятно, что число таких строк совпадает с числом возможных разбиений. На каждом месте может находиться один из двух символов, все символы можно менять независимо, поэтому таких строк 2^4 = 16.
ответ. 16.
Если подмножества неразличимы, то каждое разбиение подсчитано дважды. Поэтому ответ в два раза меньше, 2^3 = 8.
Upd. В комментарии написали, что ответ якобы 10. Это не очень похоже на правду. Если не различать подмножества, то ответ не может быть больше 8. Если различать подмножества, то надо как-то отвергнуть 6 вариантов разбиения. Как это сделать, непонятно.
Можно рассматривать разбиения на непустые подмножества, т.е. отвергнуть варианты, в которых все элементы попадают в одно подмножество, а второе пусто. Если различать подмножества, получится 16 - 2 = 14 вариантов, если не различать - 7. В любом случае 10 не получается.
По теореме Кронекера-Капелли, система будем совместной тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
При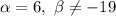 система не совместна. При
система не совместна. При 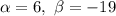 система совместна, при этом
система совместна, при этом 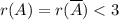 - ранг меньше числа неизвестных, то система имеет бесконечно множество решений. При
- ранг меньше числа неизвестных, то система имеет бесконечно множество решений. При 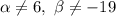 система совместна, при этом
система совместна, при этом 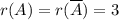 - система имеет единственное решение. При
- система имеет единственное решение. При 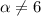 и
и 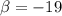 система совместна, причём система имеет единственное решение, ранг равен числу неизвестных
система совместна, причём система имеет единственное решение, ранг равен числу неизвестных