1.
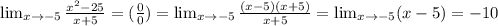
2.
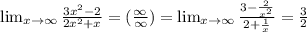
3. нет. Но не понял задания: нужно графически или аналитически определить? в любом случае график функции думаю вы сами сможете нарисовать.
4
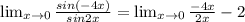
5
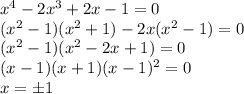
Объяснение:
Если не возникает неопределенностей (посмотрите, например, в и-нете "неопределенности пределов"), то для вычисления предела достаточно подставить вместо x, то к чему он стремится. Иначе, если появляются неопределенности, нужно их раскрыть(в этом все решение пределов). Есть множество методов решения различных неопределенностей (разложение на множители, деление числителя и знаметеля на высшую степень(только при x->∞), и т.д.).
для решения задания 4 был использован первый замечательный предел:
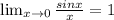
То есть в некоторых случаях можно сказать, что sinx ~ x, при x->0.
Есть брать любые точки: