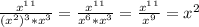
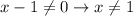
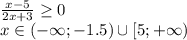
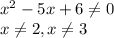
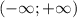(знаменатель в ноль не обращается) - симметричное множество.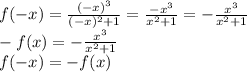
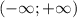(ограничений нет) - симметричное множество.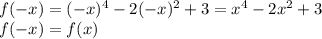
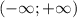(ограничений нет) - симметричное множество.
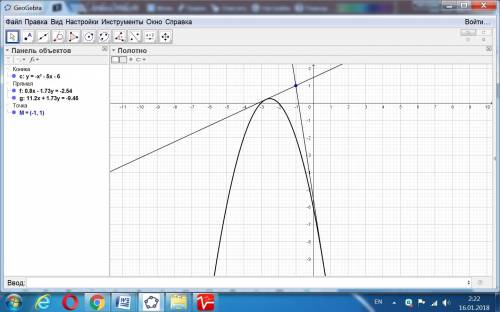
Касательная задается уравнением:
y = f ’(x₀) · (x − x₀) + f (x₀)
Здесь f ’(x₀) — значение производной в точке x₀, а f (x₀) — значение самой функции.
Находим производную в точке х₀:
f'(x₀) = -2x₀ - 5.
Функция в точке х₀ имеет вид: f(x₀) = -х₀² - 5х₀ - 6.
Тогда уравнение касательной будет таким:
у = (-2х₀ - 5)*(х - х₀) - х₀² - 5х₀ - 6.
Раскроем скобки и приведём подобные:
у = -2х*х₀- 5х + 2х₀² + 5х₀ - х₀² - 5х₀ - 6.
у = х₀² -2х*х₀ - 5х - 6.
Так как касательная проходит через точку М, то подставим её координаты в полученное уравнение.
1 = х₀² + 2х₀ + 5 - 6.
Получаем квадратное уравнение х₀² + 2х₀ - 2 = 0.
Решаем его, считая х₀ как х.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=2^2-4*1*(-2)=4-4*(-2)=4-(-4*2)=4-(-8)=4+8=12;
Дискриминант больше 0, уравнение имеет 2 корня:
x₁ = (√12-2)/(2*1) = √12/2-2/2 = √12/2-1 = √3 - 1 ≈ 0.73205081;
x₂ = (-√12-2)/(2*1) = -√12/2-2/2 = -√12/2-1 = -√3 - 1 ≈ -2.73205081.
Теперь, зная точки касания, можно составить уравнения касательных.
f'(x₀) = -2x₀ - 5 = -2(√3 - 1) - 5 = -2√3 - 3.
f(x₀) = -х₀² - 5х₀ - 6 = -(√3 - 1)² - 5(√3 - 1) - 6 =
= -(3 - 2√3 + 1) - 5√3 + 5 - 6 = -3√3 - 5.
y = f ’(x₀) · (x − x₀) + f (x₀) = (-2√3 - 3)(x + 2√3 + 3) - 3√3 - 5.
После упрощения получаем общее уравнение первой касательной:
0,8x - 1,73y + 2,54 = 0.
