в случае неравномерного движения, когда v≠const
v(t)=ds/dt
ds=v(t)dt
t₂
s=∫ v(t)dt
t₁
нужно найти путь, пройденный точкой за седьмую секунду. это период времени с 6 секунды по 7 секунду. для нашего случая можно записать:
₇ ₇
s=∫(3t²+6t-1)dt =t³+3t²-t | =(7³+3*7²-³+3*6²-6)= 483-318 =165 (м)
⁶ ⁶
ответ: 165 м
подробнее - на -
: 
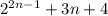
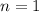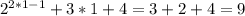
, где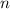 
- любое натуральное число.
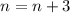то покажем, что наше допущение также правда. 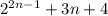- делится на 9 (известно из шага 2)
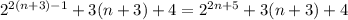- доказываем (с гипотезой, что случай n=n - прав)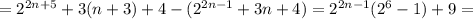
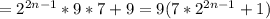
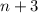, а это подтверждает гипотезу.
Р=2х+ 288/х.
Знайдемо похидну:
Рштрих=2-288/х².
Приривняэмо похидну до нуля и знайдемо критични точки:
2-288/х²=0
-288/х²=-2
х²=288/2
х²=144
х=12 - точка-претендент на екстремум, але, оскильки похидна, проходячи через нейи, миняэ знак з минуса на плюс, то 12 - точка минимума.
Видповидь: Вони мають бути ривними 12 сантиметрам (це квадрат).