Объяснение:
1) Завдання
Пусть х буде перше число, тоді друге у.
Сума їх дорівнює 70, тобто х+у=70
А різниця 28, тобто х-у=28
Складаємо систему рівнянь
{х+у=70
х-у=28
Метод додавання
2х=98
х=98:2
х=49 перше число
Підставляємо значення х в одно із рівнянь
х+у=70
49+у=70
у=70-49
у=21 друге число
Відповідь: (49;21)
2) завдання
Пусть х буде коштувати 1 ручка, тоді у буде коштувати 1 олівець
5 ручок і 4 олівці коштують 50 грн, тобто 5х+4у=50
3 ручкі дорожче за 2 олівця на 8грн.
тобто 3х-2у=8
Складаємо систему рівнянь
{5х+4у=50
3х-2у=8 множимо на 2
{5х+4у=50
6х-4у=16
Метод додавання
11х=66
х=66/11
х=6 грн. коштує 1 ручка
Підставляємо значення х в одно із рівнянь
3х-2у=8
3*6-2у=8
18-2у=8
-2у=8-18
-2у=-10
у=10/2
у=5 грн коштує 1 олівець
Відповідь: 5грн. коштує 1 олівець, 6грн. коштує 1 ручка.
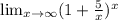
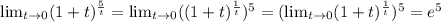

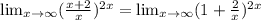
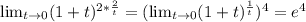

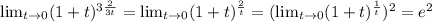
=3ав(3+4ав)
=4mn(6-4mn)
=21bc