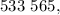 которая должна выражать дату (в каком-то неизвестном представлении).
которая должна выражать дату (в каком-то неизвестном представлении).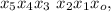


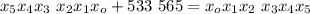 ;
;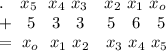

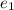 – возможная добавочная единица, уходящая из первого
– возможная добавочная единица, уходящая из первого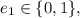
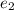 – возможная добавочная единица, уходящая из второго
– возможная добавочная единица, уходящая из второго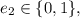
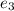 – возможная добавочная единица,
– возможная добавочная единица,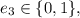
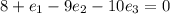 ;
;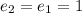 и при
и при  ;
;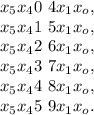
 поскольку
поскольку 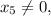 так как с этой цифры начинается разностное число.
так как с этой цифры начинается разностное число. поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.
поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.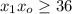 .
.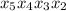 .
.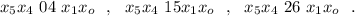
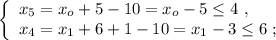

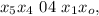
 может играть роль апреля.
может играть роль апреля.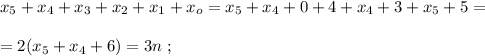
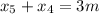 ;
;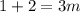 ;
;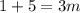 ;
;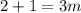 ;
; ;
;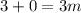 ;
;
 – дата 12/04/56 г.
– дата 12/04/56 г. – дата 15/04/86 г.
– дата 15/04/86 г.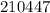 – дата 21/04/47 г.
– дата 21/04/47 г.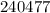 – дата 24/04/77 г.
– дата 24/04/77 г.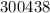 – дата 24/04/38 г.
– дата 24/04/38 г.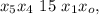
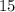 может играть только роль числа месяца (дня).
может играть только роль числа месяца (дня).
 ;
;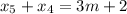 ;
;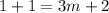 ;
;
 – дата 11/15/46 г.
– дата 11/15/46 г.

Рассмотрим вертикальные линии и горизонтальные. Каждую из них диагональ пересекает ровно один раз. При этом каждое пересечение вертикальной или горизонтальной линии соответствует пересечению двух (соседних) клеток. Посчитаем сумму вертикальных ( ) и горизонтальных клеток (
) и горизонтальных клеток (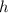 ): каждая клетка, которую пересекают (кроме двух крайних), считается дважды (она дважды участвует в паре), но также каждое пересечение считается дважды. Поэтому
): каждая клетка, которую пересекают (кроме двух крайних), считается дважды (она дважды участвует в паре), но также каждое пересечение считается дважды. Поэтому 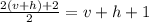 есть количество пересеченных клеток (мы добавили двойку в числителе вот почему: 2(v+h) - это удвоенное количество средних клеток (т.е. не крайних), а крайние посчитаны только один раз. Добавляя 2, мы считаем и крайние два раза. Теперь все клетки посчитаны дважды — можем делить на 2)
есть количество пересеченных клеток (мы добавили двойку в числителе вот почему: 2(v+h) - это удвоенное количество средних клеток (т.е. не крайних), а крайние посчитаны только один раз. Добавляя 2, мы считаем и крайние два раза. Теперь все клетки посчитаны дважды — можем делить на 2)
Пусть дан прямоугольник  , причем числа
, причем числа 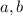 не имеют общих делителей (иначе какая-то клетка пересекалась бы по вершине — мы ее не считали). Тогда
не имеют общих делителей (иначе какая-то клетка пересекалась бы по вершине — мы ее не считали). Тогда 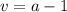 ,
, 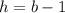 . Получаем
. Получаем 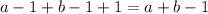 пересеченная клетка. Поскольку числа 239 и 566 не имеют общих делителей, к ним применима эта формула. Получаем, что диагональ пересекает 239+566-1=804 клетки
пересеченная клетка. Поскольку числа 239 и 566 не имеют общих делителей, к ним применима эта формула. Получаем, что диагональ пересекает 239+566-1=804 клетки
y^3 - y^5=y^3*1-y^3* y^2=y^3 (1-y^2)=y^3 (1-y)(1+y)
используя вынос общего множителя и формулу разности квадратов