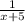раб./час.
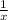раб./час.
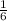раб./час. 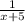+ 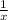= 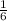(умножим на 6х(х+5), чтобы избавиться от дробей)
+ 
= 
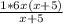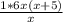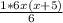
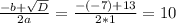
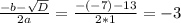- не подходит, поскольку х<0
с=200
р=160
Объяснение:
Известно, что 30% числа c на 20 больше, чем 25% числа p, а 30% числа p на 8 больше, чем 20% числа c. Найди числа c и p.
По условию задачи составляем систему уравнений:
0,3c-0,25p=20
0,3p-0,2c=8
Выразим c через p в первом уравнении:
0,3c=20+0,25p
c=(20+0,25p)/0,3
Подставим значение с во второе уравнение и вычислим р:
0,3р-0,2[(20+0,25p)/0,3]=8
Умножим уравнение на 0,3, чтобы избавиться от дроби:
0,3*0,3р-0,2(20+0,25р)=0,3*8
0,09р-4-0,05р=2,4
Приводим подобные члены:
0,04р=2,4+4
0,04р=6,4
р=6,4/0,04
р=160
с=(20+0,25*160)/0,3
с=(20+40)/0,3
с=60/0,3
с=200
Получилась совокупность из двух уравнений, задающих две прямые y = x и y = 1 - x. Прямые можно построить по двум точкам, например, первая прямая проходит через точки (0, 0) и (1/2, 1/2); вторая прямая проходит через точки (0, 1) и (1/2, 1/2).
Замечу, что формулировка задания не вполне корректна: уравнение не задает функцию, каждому значению x ≠ 1/2 отвечают 2 различных значения y.