В обеих точках функция непрерывна
Объяснение:
Для ответа на данный вопрос найдём пределы слева и справа от указанных точек, если пределы совпадают, то функция в данной точке непрерывна, если не совпадают, то функция имеет разрыв первого рода, а если хотя бы один из пределов равен бесконечности или не существует, то в данной точке функция имеет разрыв второго рода.
для x = 0
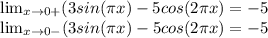
Как видим, пределы слева и справа совпадают, следовательно f(0) непрерывна
для x = 1
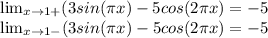
Снова видим, что пределы совпадают, следовательно и при f(1) функция непрерывна.
В решении.
Объяснение:
2. Чи належить графіку функції у = х² - х +1 точка:
1) А (0 ;-1)
2) В(0; 1)
3) С(2;0)
4) D(1;1)
5) Е(-2;6)
Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение. Если левая часть равна правой, то принадлежит, и наоборот.
1) у = х² - х +1 А(0; -1)
-1 = 0² - 0 + 1
-1 ≠ 1, не принадлежит.
2) у = х² - х +1 В(0; 1)
1 = 0² - 0 + 1
1 = 1, принадлежит.
3) у = х² - х +1 С(2; 0)
0 = 2² - 2 + 1
0 ≠ 3, не принадлежит.
4) у = х² - х +1 D(1; 1)
1 = 1² - 1 + 1
1 = 1, принадлежит.
5) у = х² - х +1 Е(-2; 6)
6 = (-2)² -(-2) + 1
6 ≠ 7, не принадлежит.
1) введём новое обозначение, пусть х^2 это у, тогда у^2-14у-32=0, отсюда следует, что D=(14^2)-4*1*(-32)=196+128=324=18^2, отсюда у=(14-18)/2=-2 и у=(14+18)/2=16
вернумся к замене, получается, что х^2=-2, но решений этого уравнения нет, так как корень из неотрицательного числа не вычисляется, а вот уравнение х^2=16 решается, получается х=4 и х=-4
2)сперва разложип по формуле выражение, а потом раскроем скобки и получится:
1+2х^2+х^4+0,5+0,5х^2-5=0 приведём подобные:х^4+2,5х^2-3,5=0
опять введём новое обозначение, пусть х^2=у, тогда получим уравнение: у^2+2,5e-3,5=0, найдум дискриминант: D=6,25-4*1*(-3,5)=20,25=4,5^2, отсюда у=(-2,5-4,5)/2=-3,5 и у=(-2,5+4,5)/2=1, вернёмся к замене .но первый у не берём, потому что из отрицательного числа корень не находится, по-этому, х^2=1, отсюда х=1 и х=-1
3) введём новое обозначение пусть 2х-7 равно у, тогда получим уравнение у^2-11у+30=0, дискриминант тогда равен D=121-4*1*30=1, тогда у=(11-1)/2=5 и у=(11+1)/2=6, вернёмся к замене, тогда6 2х-7=5 и х=6, 2х-7=6 и х=6,5
4)введём новое обозначение пусть 6х+1=у, тогда получим уравнение у^2+2у-24=0, D=4-4*1*(-24)=100=10^2, тогда у=(-2-10)/2=-6 и у=(-2+10)/2=4, вернёмся к замене тогда 6х+1=-6, х=-1целая 1/6 , 6х+1=4, х=0,5
5)пусть 1+х^2=у, тогда у^2+0,5у-5=0 ,D=0,25-4*1*(-5)=20,25=4,5^2, тогда у=(-0,5-4,5)/2=-2,5 и у=(-0,5+4,5)/2=2, тогда 1+х^2=-2,5, но это уравнение не имеет решений, так как корень из неотрицательного числа не находится, 1+х^2=2, х=1 и х=-1