Объяснение:
Системы линейных уравнений решаются тремя
1) Методом подстановки;
2) Методом сложения;
3) Графическим методом.
Мы будем решать системы сложения.
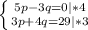
Первое уравнение мы домножим на 4, второе - на 3.
Мы домножаем уравнения для того, чтобы уравнять переменные. (Иначе мы не решим систему).
Получим обновленную систему уравнений:
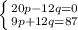
12q и -12q взаимно уничтожатся с сложения. Остальные переменные тоже складываются.
В итоге имеем:
29p = 87
p = 3
Мы нашли значение переменной p. Переписываем это значение и берем одно из уравнений системы, которая была у нас сначала:
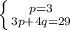
Я взял выражение 3p + 4q потому, что здесь все знаки положительные.
Подставляем значение p:
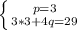
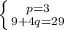
Имеем:
4q = 20
q = 5
Система №2.
(Попробуй решить самостоятельно).
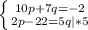
Домножаем второе уравнение на 5.
Имеем:
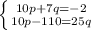
-110 переносим вправо, 25q - влево.
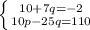
10p уничтожится вычитанием. Следовательно, уравнения вычитаем.
Имеем:
32q = -112
q = -3,5
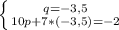
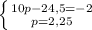
Здесь делается все то же самое, что и в первой системе.
Весь основной материал я рассказал в начале.
Задача решена.
Понятно ли я объяснил задачи?
Запишем ее так, чтобы было видно, что эти уравнения – функции:
Строим графики прямых в одной системе координат: легче всего сделать это по точкам (берете x = 1; 2; 3; 4; -1; 2; -3; -4; 0 и т.д., пока не будет достаточно, чтобы построить график точно, но в случае с прямыми достаточно двух точек :)) (график приложила) и смотрите точку пересечения. Это (3; 2) – ваш ответ.
ответ: (3; 2).