а) вероятность того, что первый шар черный 5/7, вероятность, что второй шар черный 4/6, вероятность того, что вынуты два черных шара 5/7·4/6=10/21=0,476190..
б) вероятность того, что первый шар красный равна 2/7, вероятность ого, что второй шар красный равна 1/6, вероятность того, что оба шара красные равна
2/7·1/6=1/21=0,
в) вероятность того, что первый шар черный равна 5/7, вероятность того, что второй шар красный равна 2/6, вероятность того, что первый черный, второй красный равна
5/7·2/6=5/21
вероятность того, что первый шар красный равна 2/7, вероятность того, что второй шар черный равна 5/6, вероятность того, что первый шар красный, второй черный равна 2/7·5/6=5/21
вероятность того , что шары разных цветов равна 5/21+5/21=10/21=0,
Число р при делении на 3 может давать остатки 0,1 или 2.
Если число р при делении на 3 дает остаток 1, то оно имеет вид
p=3k+1, где k - некоторое целое число
Но тогда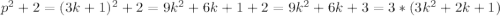 
, а значит число 
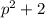не является простым. Значит такой случай невозможен
Если число р при делении на 3 дает остаток 2, то оно имеет вид
p=3k+2, где k - некоторое целое число
Но тогда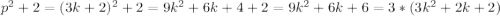 
, а значит число 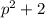не является простым. Значит такой случай невозможен
Значит число р при делении на 3 дает остаток 0, а значит число р делится нацело на 3. Число р делится нацело на 3 и является простым, значит число р может равняться только числу 3.
При р=3: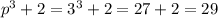 
- простое, что и требовалось доказать.Доказано
Время скорого поезда: \dfrac{S}{v} = \dfrac{400}{x}vS=x400
Время товарного поезда: \dfrac{S}{v} = \dfrac{400}{x-20}vS=x−20400
Разница между ними - 1 час
\begin{lgathered}\dfrac{400}{x-20}- \dfrac{400}{x}=1\\ \\ \\ \dfrac{1}{x-20}-\dfrac{1}{x}=\dfrac{1}{400}\bigg|\,\, \cdot400x(x-20)\\ \\ \\ 400x-400(x-20)=x(x-20)\\ 400x-400x+8000=x^2-20x\\ x^2-20x=8000\\ x^2-20x+100-100=8000\\ (x-10)^2=8100\\ x-10=\pm90\end{lgathered}x−20400−x400=1x−201−x1=4001∣∣∣∣⋅400x(x−20)400x−400(x−20)=x(x−20)400x−400x+8000=x2−20xx2−20x=8000x2−20x+100−100=8000(x−10)2=8100x−10=±90