Запишем систему уравнений в исходном виде:
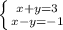
А) Подставим пару чисел (1;1):
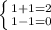
Отсюда делаем вывод, что пара чисел (1;1) не является решением данной системы уравнений, так как не удовлетворяет ни 1 уравнению системы.
Б) Подставим числа (1;2)
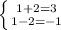
Отсюда делаем вывод, что пара чисел (1;2) является решением данной системы уравнений, так как удовлетворяет обоим уравнениям системы.
В) Подставим пару чисел (2;1):
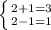
Отсюда делаем вывод, что пара чисел (2;1) не является решением данной системы уравнений, так как данная пара чисел не удовлетворяет второму уравнению.
Г) Подставим пару чисел (2;2):
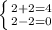
Отсюда делаем вывод, что пара чисел (2;2) не является решением данной системы уравнений, так как не удовлетворяет ни 1 уравнению системы.
1) для начала решим уравнение lg((x-2)/(4-x))=0 <=> (x-2)/(4-x)=10^0=1 <=> (x-2-4+x)/(4-x)=0 <=> x=3 и x<>4. Так как это выражение стоит в знаменателе, то и x<>3.
2) при этом мы знаем, что логарифм числа >0 => (x-2)/(4-x)>0 <=> 2 < x < 4
3) расположим значения из п. (1) на координатной прямой х с условиями (2). как видим получилось два промежутка: 2<x<3 и 3<x<4, что и явл-ся ответом.