(х + 6) * (х - 3)
Объяснение:
Розв'яжемо цей квадратний тричлен як квадратне рівняння:
х^2 + 3х - 18 = 0
За теоремою Вієта:
х1 + х2 = -3
х1 * х2 = -18
Підбираємо такі значення х1 і х2, щоб вони відповідали цій системі рівнянь. Це (-6) і 3.
Скористаємось формулою розкладання квадратного тричлена на множники, а саме:
ах^2 + bx + c = a * (x - x1) * (x - x2)
Виходячи з того, ща в нашому рівнянні а=1, х1 = -6, х2 = 3, підставимо ці значення в формулу:
a * (x - x1) * (x - x2) = 1*(х - (-6)) * (х - 3) = (х + 6) * (х - 3)
Маємо квадратний тричлен, розкладений на множники
Завдання 1:
Координати точки, яка належить графіку функції (або через яку проходить графік), будуть задовільняти формулу, якою ця функція задана.
Підставимо координати точки В (-2; у) у формулу: абсцису замість х, ординату замість у.
у = -3 ∙ (-2).
Тепер можемо обчислити ординату:
у = 6.
Відповідь: 6.
Завдання 2:
Підставимо координати точки N (-4; 9) у формулу: : абсцису замість х, ординату замість у.
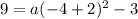
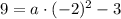
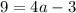
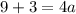
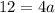
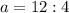
a = 3.
Відповідь: 3.
Завдання 3:
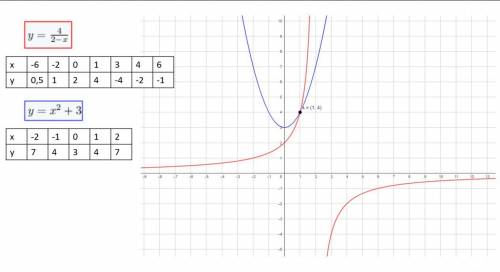
Щоб вирішити рівняння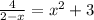 
графічно, треба побудувати графіки двох функцій:
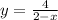та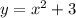 
.
Коренями рівняння будуть абсциси точок перетину цих графіків.
Побудуємо графіки, створивши таблицю точок, що належать їм (див. малюнок).
Точка перетину графіків А (1;4).
х = 1.
Відповідь: 1.
