Question

Задание 2. Докажите, что разность квадратов двух последовательных нечетных чисел

делится на 8.

Для начала составим выражение, о котором говорится в задании. Если четное число

можно записать при переменной как 2, то нечетное число будет выглядеть как

2n + 1.

1-ое нечетное число: 2n + 1

2-ое нечетное число: 2n + 3

Разность квадратов этих чисел: (2 + 3)

2 − (2 + 1)

2

Теперь необходимо доказать, что данное выражение кратно 8. Попробуйте сделать это

самостоятельно. Здесь неважно то, как вы начнете действовать: вы можете

воспользоваться формулой разности квадратов, а можно взять и у данное

выражение.

Задание 3. Докажите, что если к произведению трёх последовательных целых чисел

прибавить среднее из них, то полученная сумма будет равна кубу среднего числа.

Подсказка:

Рассмотрим каждое выражение, о котором говорится в задаче.

Первое число:

Второе число: ( n+ 1)

Третье число: (n + 2)

Их произведение:n ( n+ 1)(n + 2)

Прибавим среднее число и получим: (n + 1)(n + 2) + (n + 1)

Куб среднего числа: (n + 1)

3

Теперь можем составить тождество, которое необходимо доказать:

n(n + 1)( n+ 2) + (n + 1) = (n + 1)3

Answer 1

$2)\; \; (2n+3)^2-(2n+1)^2=\Big((2n+3)-(2n+1)\Big)\Big((2n+3)+(2n+1)\Big)=\\\\=(3-1)(4n+4)=2\cdot 4(n+1)=8\cdot (n+1)\\\\8(n+1)\, \vdots \; 8$

Если число можно представить в виде произведения , где одним из множителей является  8, то это число делится на 8 .

$3)\; \; n\underline {(n+1)}(n+2)+\underline {(n+1)}=(n+1)\cdot \Big(n(n+2)+1\Big)=\\\\=(n+1)\underline {(n^2+2n+1)}=(n+1)\underline {(n+1)^2}=(n+1)^3$

Если к произведению трёх последовательных чисел прибавить среднее из них, то полученная сумма равна кубу среднего числа.

Answer 2

Задание 2

Обозначим первое число как 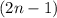$(2n-1)$, а следующее за ним как 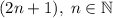$(2n+1), \; n \in \mathbb N$. Раскроем разность квадратов по формуле $a^2-b^2=(a-b)(a+b)$:

$(2n-1)^2-(2n+1)^2=(2n-1-(2n+1))(2n-1+2n+1)=\\=-2 \cdot 4n=-8n$

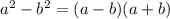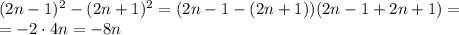
Один из множителей делится на 8, а значит, и всё число делится на 8.

Задание 3

Запишем три последовательных числа как 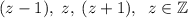$(z-1), \; z, \; (z+1), \; \; z \in \mathbb Z$. Составим выражение из условия:

$(z-1) \cdot z \cdot (z+1)+z=(z^2-1) \cdot z+z=z(z^2-1+1)= z \cdot z^2=z^3.$

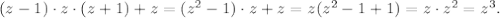
Что и требовалось доказать.