Для начала выясним, что же будет графиком этой функции? В данном случае парабола, при чем, т.к. перед x^2 стоит знак "-", то ветви направлены вниз. Значит, эта функция будет принимать значения от минус бесконечности, до ординаты вершины параболы. Задание сводится к тому, чтобы найти координаты вершины. Приступим.
Абсциссу вершины параболы находив по формуле:
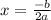, где b-коэффициент перед x, а-коэффициент перед x^2.
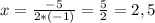
Теперь подставим значение икса в нашу функцию и найдем ординату вершины параболы
y=-(2,5)^2 +5*2,5-9=-6,25 +12,5-9=-6,25+3,5=-2,75=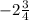
Значит координаты вершины параболы (2,5; -2,75)
Следовательно, функция принимает значения ![(- \infty;-2\frac{3}{4}]](/tpl/images/0091/8443/7c376.png)
15
Объяснение:
Пусть скорость(v) первого теплохода х км/ч, тогда v второго теплохода х+3 км/ч(т.к по условию скорость второго теплохода на 3 км/ч больше скорости первого)
чтобы найти время которое понадобится первому теплоходу разделим расстояние на его скорость 180/x часов известно, что второму теплоходу понадобится с учётом его скорости на 2 часа меньше, т.е время которое потратит второй теплоход на дорогу 180/(х+3) будет равно времени первого теплохода, из которого вычли 2 часа
составим уравнение(/ обозначает черту дроби)
180/х - 2=180/(х+3)
неизвестные влево, известные вправо
180/х - 180/(х+3)=2
находим общий знаменатель
(180х + 540 - 180х)/(х²+3х)=2
умножим обе части равенства на х²+3х
540=2х²+6х
Поделим все на два(это необязательный шаг, он нужен для упрощения вычислений)
270=х²+3х
переносим все в одну сторону
0=х²+3х-270
находим дискриминант
D=9+270*4=9+1080=1089
x1,x2=(-3±√D)/2= (-3±33)/2
х1 =15
х2= -18 сторонний корень т.к отрицательное число
Скорость первого теплохода 15
А все числа во второй скобки перемножаем на число перед скобкой.
( а + 6 )^2 - 2а ( 3 - 2а ) = а^2 + 12а + 36 - 6а + 4а^2 = 5а^2 + 6а + 36.
Удачи)))