Лінійні рівняння з двома змінними
Лінійним рівнянням з двома змінними та називається рівняння виду (або виду ).
Приклад :
лінійні рівняння.
Якщо в лівій частині рівняння і , то це рівняння першого степеня з двома змінними.
Приклад:
- лінійне рівняння.
- рівняння першого степеня з двома змінними.
Розв'язком рівняння з двома змінними і називається кожна пара чисел ( ; ), яка перетворює це рівняння на правильну числову рівність.
Приклад:
Для рівняння пара ( 1; 2) є розв'язком, оскільки при і одержуємо - правильна рівність. Пара (0; 1) не є розв'язком заданого рівняння, оскільки при і одержуємо ; - неправильна рівність.
Два рівняння з двома змінними називаються рівносильними, якщо вони мають одні й ті самі розв'язки або обидва рівняння не мають розв'язків.
Приклад:
Рівняння і - рівносильні.
Властивості рівносильних рівнянь з двома змінними
Якщо обидві частини рівняння з двома змінними помножити або поділити на одне і те саме число, яке не дорівнює нулю, то одержимо рівняння , рівносильне даному.
Приклад :
Рівняння і - рівносильні (друге можна одержати з першого множенням на 2).
Якщо будь-який член рівняння з двома змінними перенести з однієї частини рівняння в іншу з протилежним знаком, то одержимо рівняння, рівносильне даному.
Приклад:
Рівняння і - рівносильні.
Графік лінійного рівняння з двома змінними
На координатній площині графіком лінійного рівняння називається множина точок, координати яких задовольняють даному рівнянню.
Якщо чи , графіком заданого рівняння є пряма, і для її побудови досить отримати будь - які дві точки цієї прямої.
Приклад :
Графіком рівняння є пряма
Якщо і , графіком заданого рівняння є пряма, паралельна осі
Приклад :
Графіком рівняння є пряма
Якщо і , графіком заданого рівняння є пряма, паралельна осі
Приклад :
Графіком рівняння є пряма .
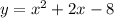
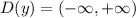
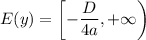 - где D дискриминант.
- где D дискриминант.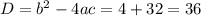
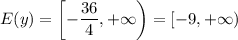
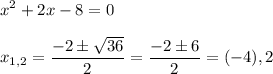



![(-\infty,-1]](/tpl/images/0467/5865/91666.png)
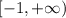

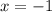
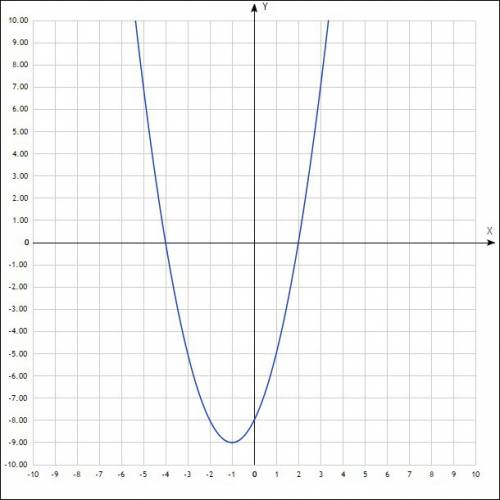
x и y -двух и трехместные байдарки
2x+3y=29
x+y=12 2x+2y=24 y=5 2x=29-15=14 x=7
было 7 двухместных
5 трехместных