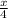 + 3 =
+ 3 = 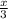 + 2
+ 2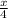 -
- 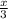 = 2 - 3
= 2 - 3 = -1
= -1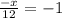
ответ: 1) ответ-нет.
На плоскости у двух прямых всего два варианта – прямые пересекаются или не пересекаются (параллельны). Если пересекаются, то имеют только одну общую точку.
2) ответ -нет
Через точку плоскости можно провести множество прямых, не принадлежащих данной плоскости.
Через точку плоскости можно провести множество прямых, на данной плоскости.
3) ответ-нет.
Если две прямые пересекаются, то делят плоскость на 4 части
Если две прямые параллельны, то они делят плоскость на 3 части.
4) ответ-нет.
Точка, делящая отрезок на две равные части, называется серединой отрезка.
5) ответ-нет
Если точки A, B, C лежат на одной прямой, причём точка В лежит между точками А и С, то имеет место равенство: AB+BC=AC
v - знак квадратного корня.
v(3x-2)< =x одз: 3x-2> =0; x> =2/3
в левой части неравенства стоит квадратный корень,который принимает только неотрицательные значения,поэтому правая часть неравенства тем более должна быть неотрицательной: x> =0.
возведем обе части в квадрат:
3x-2< =x^2
3x-2-x^2< =0
x^2-3x+2> =0
x^2-3x+2=0
d=(-3)^2-4*1*2=1
x1=(3-1)/2=1; x2=(3+1)/2=2
++
с учетом одз: x e [2/3; 1] u [2; + беск.)
подробнее - на -
3X+36=4X+24
3X-4X=24-36
-X= -12
X=12