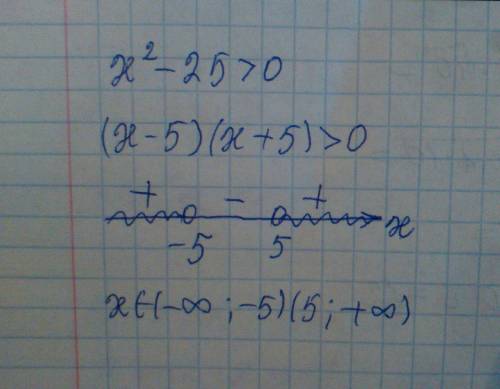
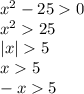
Для острых углов известно соотношение sinα<α<tgα . α=1/(n+6) стремится к 0 при n->∞.
tg1/(n+6)>1/(n+6).
Исходный ряд сравним с рядом ,общий член которого 1/(n+6).Этот ряд расходящийся, так как его можно сравнить с расходящимся обобщённо-гармоническим рядом ∑1/n : lim (1/n)/(1/n+6)=1≠0 при n->∞ ⇒ оба ряда ∑1/n и ∑1/(n+6) расходятся.
Ряд ∑1/(n+6) является минорантным, а ряд ∑tg1/(n+6) мажорантным. Из расходимости минорантного ряда следует расходимость мажорантного. ⇒∑tg1/(n+6) - расходящийся ряд.
1) Імовірність випадення числа меншого від 5 = 4/6=2/3, бо числа 1 2 3 4 задовольняют умову, а всього на кубику 6 чисел.
Імовірність випадення числа більшого за 4 = 2/6=1/3, бо числа 5 6 задовольняють умову, а всього на кубику 6 чисел.
Для отримання результату помножимо ймовірність виконання умови при першому кидку на ймовірність виконання умови при другому кидку: 2/3*1/3=2/9
2)Імовірність виконнная умови 5/6 при першому кидку і 1/6 при другому. Отримуємо 1/6*5/6=5/36
3)Імовірність випадення на кубику при першому киданні числа більшого ніж при другому киданні дорівнює 1/2-1/6=1/3, оскільки 1/6-імовірність випадення дубля. Наприклад, перший раз випало число 1. Імовірність випадення того самого числа при другому киданні дорівнює 1/6 (6 варіантів 1 з яких нас задовольняє).1/2 ми вказуємо, бо при киданні використовується один і той самий кубик, і кількість випадків, які нас задовольняють удвічі менша за тотальну кількість імовірних подій, тобто імовірність симетрична.
Отже, відповідь: 1/3