Дано: прямоугольный Δ
a; b - катеты
S=90 см²
S₁+S₂ = а²+b² =369 см₂
a-? b-?
Решение
1) Первое уравнение получаем из условия:
а²+b² = 369
2) Площадь прямоугольного треугольника равна половине произведения катетов, получаем второе уравнение:
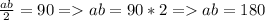
3) Решаем систему: (a>0; b>0)
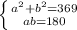
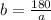
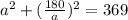
a≠0
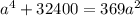
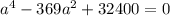
Замена: а²=t ( t > 0)
Решаем уравнение:
t² - 369t + 32400 = 0
D = 369² - 4·1·32400 = 136161 - 129600 = 6561 = 81²
t₁ = (369-81)/2 = 144
t₂ = (369+81)/2 = 225
Обратная замена:
При t₁ = 144 => a² = 144 => a₁ = - √144 = - 12 < 0
a₂ = √144 = 12 > 0
При t₂ = 225 => a² = 225 => a₃ = - √225 = - 15 < 0
a₄ = √225 = 15 > 0
Зная а₁=12 и а₂ = 15, найдем b
b₁ = 180/12 = 15
b₂ = 180/15 = 12
Получаем два решения взаимозаменяемых:
а=12; b=15
а=15; b=12
ответ: 12 см; 15 см - катеты
Обычно линейное уравнение определяется, как уравнение вида:
ax + b = 0 (основная формула линейного ура-я), где а и b – любые числа.
Например: 2х+7=0, в данном случае а=2, b=7.
Теперь рассмотрим пример с подробным решением:
х - 3 = 2 - 4х (переносим все неизвестные влево (значением с буквами), известные вправо (обычные цифры) , при этом меняем знаки на противоположные, получим:
х+4х=2+3 (вычисляем), получаем такое вот сокращённое ура-е:
5х=5 (чтобы найти х мы должны: правую часть разделить на цифру при переменной х):
х=5:5 , х=1
основание степени а=0,3. 0<0,3<1 => функция убывающая на всей области определения.
б). y=log₀,₃x логарифмическая функция
основание логарифма а=0,3. 0<0,3<1=> функция убывающая на всей области определения.
в). y=x² квадратичная функция, график -парабола, ветви параболы направлены вверх. координаты вершины (0;0)
функция возрастает при х∈(-∞;0), функция убывает при х∈(0;∞)
г). у=1+х, у=1*х+1 - линейная функция. k=1. k>0 => функция возрастающая на всей области определения