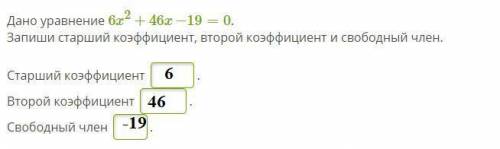
№1 (ответ на фото)
Квадратным уравнением называют уравнение вида ах²+bх+с=0, где коэффициенты а, b, с - любые действительные числа, причём, а≠0. Коэффициенты а, b, с, различают по названиям: а - первый или старший коэффициент; b - второй или коэффициент при х; с - свободный член, свободен от переменной х
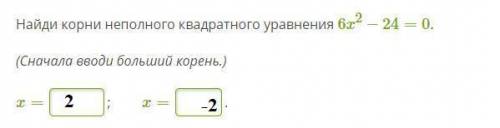
№2 ( ответ на фото)
Приведенное квадратное уравнение – уравнение вида , первый коэффициент которого равен единице
№3.
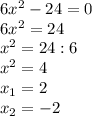
ответ: ±2
№4.
8x²+6x+9=0
a=8 b=6 c=9
D=b^2-4ac=6^2-4*8*9=36-288=-252
№5
x²+14x-8=0
D=14²-4*1*(-8)=196+32=228
√D=√228=2√57
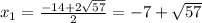
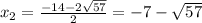


Пусть в квадратном уравнении значение a (возле x^2) = 1, тогда b (возле x) = -2 * (a - 1), а c = -2a + 1. Согласно теореме Виетта:
x(1) * x(2) = c/a
x(1) + x(2) = -b/a
Если один из корней уравнения положительный, а другой - отрицательный, то значение c/a отрицательное, так как при умножении положительных чисел на отрицательные произведение также отрицательное (меньше, чем 0). Тогда:
c/a < 0
(-2a+1)/1 < 0
-2a + 1 < 0
-2a < 0 - 1
-2a < -1
a > -1 : (-2)
a > 0,5
ответ: квадратное уравнение будет иметь положительный и отрицательный корни при a > 0,5
Подробнее - на -
Объяснение:
________________