По условию задачи, если к некоторому палиндрому (х+3) прибавить 2, то получится также палиндром (х+5). Найдем этот палиндром (х+3).
Заметим, что если при прибавлении к числу 2 не произошло перехода в старшие разряды, то получившееся число не будет палиндромом. Значит, последняя цифра числа (х+3) равна 8 или 9. Тогда, после прибавления к такому числу 2, его последняя цифра станет равной 0 или 1 соответственно. Но по смыслу палиндрома, эта же цифра должна являться и его первой цифрой. Единственный возможный вариант - произошел переход через все разряды вплоть до старшего в исходном числе.
Единственное число-палиндром, при прибавлении к которому 2 произойдет переход по всем разрядам - это число 9999. Заметим, что результат суммы 9999+2=10001 - палиндром.
Таким образом, число (х+3) найдено и равно 9999.
Значит, х=9996.
ответ: 9996
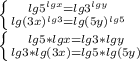
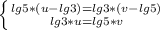
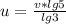
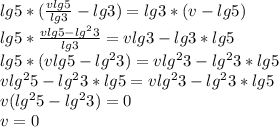
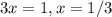 и
и 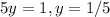
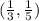
1)
6(p-q)(p+q)-6p^2+12q^2=6p²-6g²-6p²+12g²=6g²
2)
(х-4)(х+4)-х^2=2х
x²-16-x²-2x=0
-2x=16
x=16/(-2)
x=-8
Проверка:
(-8-4)(-8+4)-(-8)²=2×(-8)
-12×(-4)-64=-16
-16=-16
ответ: x= -8