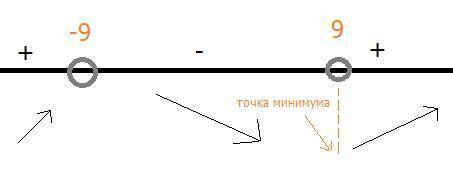
![y=2\cdot\frac1{x^3}-8 \sqrt[4]{x}](/tpl/images/0921/3336/c9e6b.png)
![y'=-\frac6{x^4}-\frac2{ \sqrt[4]{x^3} }](/tpl/images/0921/3336/a0bee.png)
1) 1/m^4
2) 2х/y
3) 6b/a - b
Объяснение:
1) m^2/a+b * a+b/m^6
a+b сокращаются, получаем
m^2 * 1/m*6
сокращаем выражение на m^2 и получаем
1/m^4
2) 16x^3/y^4 : 8x^2/y^3
переворачиваем вторую дробь и меняем знак деления на умножение
16x^3/y^4 * y^3/8x^2
сокращаем 16 и 8 на 8,получаем
2x^3/y^4 * y*3/x^2
далее сокращаем выражние на x^2
2x/y^4 * y^3
и сокращаем выражение на y^3,получаем
2х/y
3) (2a+2b) * 3b/a^2-b^2
для начала нужно разложить выражение на множители
2(a+b) * 3b/(a-b)(a+b)
сокращаем на a+b,получаем
2 * 3b/a-b
и вычисляем произведение
6b/a - b
ответ: Точка {9; 43}
Объяснение:
Чтобы найти точку минимума (ровно как и максимума) функции, необходимо взять производную от этой функции и приравнять ее к нулю. Сделаем это:
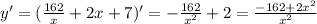
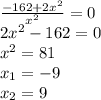
Мы получили две точки. Теперь нужно определиться, которая из них - точка минимума.
Для этого нарисуем на бумажке числовую прямую и отметим на ней получившиеся точки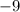 
и 
.
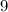Получим три промежутка:
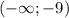
![[-9;9]](/tpl/images/1008/3639/2ae4d.png)
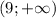
Теперь для каждого из этих промежутков выберем какое-нибудь число и подставим его в производную, чтобы определить ее знак. Получим, что производная:
положительна на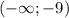отрицательна на ![[-9;0]](/tpl/images/1008/3639/71867.png)
положительна на 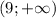Когда производная положительна на промежутке, функция возрастает, когда производная отрицательна - функция убывает.
Зарисовав соответствующие стрелочки под числовой прямой, получается, что функция имеет точку минимума в точке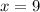 
.
Осталось подставить ее в исходную функцию для нахождения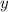 
-координаты точки.
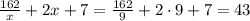
ОТВЕТ: 9;43
