Алгебра: Решите уравнение |x+3y-5|+(7x-6y+19)^2=0

Решите уравнение |x+3y-5|+(7x-6y+19)^2=0

👇

Увидеть ответ

Ответ:

Dariy69

08.02.2022

Ну я щас сразу начну без модулей.
х^2+3у+5+7х^2+36+361=0
. отсуда понятно. х=7;у=0

4,4(84 оценок)

Ответ:

m1m2m3m4m571

08.02.2022

|x+3y-5| ≥ 0 при любых х,у и (7х-6у+19)² ≥ 0 при любых х,у ⇒

|x+3y-5| + (7х-6у+19)² = 0 лишь тогда, когда одновременно выполняются равенства x+3y-5 = 0 и (7х-6у+19)² = 0. То есть надо решить систему ур-й:

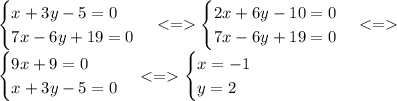
$\begin {cases} x+3y-5=0 \\ 7x-6y+19=0 \end {cases} \begin {cases} 2x+6y-10=0 \\ 7x-6y+19=0 \end {cases} \\ \begin {cases} 9x+9=0 \\ x+3y-5=0 \end {cases} \begin {cases} x=-1 \\ y=2 \end {cases}$

ответ: х=1; у=2.

Решите уравнение |x+3y-5|+(7x-6y+19)^2=0

4,4(43 оценок)

Открыть все ответы

Ответ:

Danfdffefd

08.02.2022

Исходное неравенство распадается на совокупность систем:

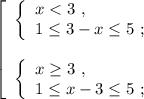
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ 1 \leq 3-x \leq 5 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 1 \leq x-3 \leq 5 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ -5 \leq x-3 \leq -1 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 1+3 \leq x \leq 5+3 \ ; \end{array}\right \end{array}\right$

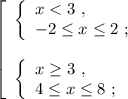
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ -2 \leq x \leq 2 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 4 \leq x \leq 8 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} x \in [ -2 ; 2 ] \ , \\ x \in [ 4 ; 8 ] \ ; \end{array}\right$

$x \in [ -2 ; 2 ] \cup [ 4 ; 8 ] \ ;$

а) неравенство эквивалентно:

$-2 \leq x \leq 2 \ ;$

$x \in [ -2 ; 2 ] \ ;$

Отрезок данного решения полностью совпадает с одним из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет 1/2 .

о т в е т :    $\frac{1}{2} = 0.5 = 50 \% \ ;$

б) неравенство эквивалентно:

$-2 \leq x-6 \leq 2 \ ;$

$6-2 \leq x \leq 2+6 \ ;$

$x \in [ 4 ; 8 ] \ ;$

Отрезок данного решения полностью совпадает с одним из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет 1/2 .

о т в е т :    $\frac{1}{2} = 0.5 = 50 \% \ ;$

в) неравенство эквивалентно:

$-1 \leq x \leq 1 \ ;$

$x \in [ -1 ; 1 ] \ ;$

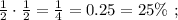
Отрезок данного решения составляет половину от одного из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет    $\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} = 0.25 = 25 \% \ ;$

о т в е т :    $\frac{1}{4} = 0.25 = 25 \% \ ;$

г) неравенство распадается на совокупность систем:

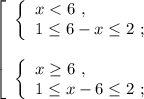
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ 1 \leq 6-x \leq 2 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 1 \leq x-6 \leq 2 \ ; \end{array}\right \end{array}\right$

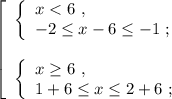
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ -2 \leq x-6 \leq -1 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 1+6 \leq x \leq 2+6 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ 4 \leq x \leq 5 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 7 \leq x \leq 8 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} x \in [ 4 ; 5 ] \ , \\ x \in [ 7 ; 8 ] \ ; \end{array}\right$

$x \in [ 4 ; 5 ] \cup [ 7 ; 8 ] \ ;$

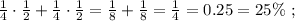
Каждый из двух отрезков данного решения составляет четверть от одного из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет    $\frac{1}{4} \cdot \frac{1}{2} + \frac{1}{4} \cdot \frac{1}{2} = \frac{1}{8} + \frac{1}{8} = \frac{1}{4} = 0.25 = 25 \% \ ;$

о т в е т :    $\frac{1}{4} = 0.25 = 25 \% \ ;$

4,4(14 оценок)

Ответ:

miao2

08.02.2022

Решение

Пусть скорость мотоциклиста x км/ч, тогда скорость велосипедиста (x–45) км/ч.

Расстояние между городами равно 60 км, тогда время в пути, которое затратили мотоциклист и велосипедист, равно соответственно 60/x часа и 60/(45 – x) часа.

Так как велосипедист был в пути на 3 часа дольше, чем мотоциклист.

Составим и решим уравнение:

60/(x – 45) - 60/x = 3

x ≠ 45, x ≠ 0

(60x – 60x + 2700 – 3x^2 + 135x) / x(x – 45) = 0

x² – 45x – 900 = 0

x₁= - 15 не удовлетворяет условию задачи

x₂ = 60

Итак, скорость мотоциклиста 60 км/ч,

60 - 45 = 15 км/ч. - скорость велосипедиста

ответ: 15 км/ч.

4,8(49 оценок)