квадрат разности: a² - 2ab + b² = (a-b)²
квадрат суммы: a² + 2ab + b² = (a+b)²
из квадрата суммы вычтем квадрат разности:
a² + 2ab + b² - (a² - 2ab + b²) = a² + 2ab + b² - a² + 2ab - b² = 4ab
ответ: 4ab
Объяснение:
1) x^2 + (5a-1)x + 4a^2 - a = 0
D = (5a-1)^2 - 4*1(4a^2 - a) = 25a^2-10a+1-16a^2+4a = 9a^2-6a+1 = (3a-1)^2

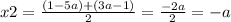
2) Мне кажется, что здесь опечатка, и должно быть так:
x^2 - (2a+3)x + 6a = 0
D = (2a+3)^2 - 4*6a = 4a^2 + 12a + 9 - 24a = 4a^2 - 12a + 9 = (2a-3)^2
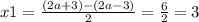
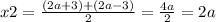
Но, если опечатки нет, тогда так:
x^2 - (2a + 3) + 6a = 0
x^2 - 2a - 3 + 6a = 0
x^2 + 4a - 3 = 0
x^2 = 3 - 4a

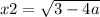
Оба корня существуют, если a ≤ 3/4
3) a^2x^2 - 10ax + 16 = 0
D = 100a^2 - 4*a^2*16 = 100a^2 - 64a^2 = 36a^2 = (6a)^2


Оба корня существуют, если a ≠ 0
4) 3(2a-1)x^2 - 2(a+1)x + 1 = 0
(6a-3)x^2 - (2a+2)x + 1 = 0
D = (2a+2)^2 - 4*(6a-3) = (4a^2 + 8a + 4) - (24a - 12) =
= 4a^2 + 8a + 4 - 24a + 12 = 4a^2 - 16a + 16 = (2a - 4)^2


Оба корня существуют, если a ≠ 1/2
1/2
Объяснение:
Попробуем разложить знаменатель на множители:
25n^2 - 5n - 6 = 0
D = 25 - 4*25*(-6) = 25 + 600 = 625 = 25^2
n1 = (5 - 25)/50 = -20/50 = -2/5
n2 = (5 + 25)/50 = 30/50 = 3/5
25n^2 - 5n - 6 = (5n + 2)(5n - 3)
Предположим, что дробь является суммой дробей:
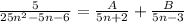
Вычислим А и В:
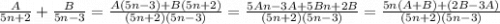
Знаменатели равны, значит, числители тоже равны. Система:
{ A + B = 0
{ 2B - 3A = 5
Решаем подстановкой:
{ A = -B
{ 2B + 3B = 5
B = 1, A = -1
Получили такую разность:
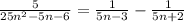
Подставляем эту разность в нашу формулу ряда:
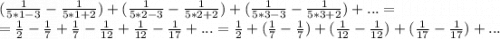
Все дроби после 1/2 сокращаются, и это продолжается бесконечно. Поэтому от всего ряда остается только первый член: 1/2
(a-b)²+x=(a+b)²
Надо найти х
x=(a+b)²-(a-b)²=a²+b²+2ab-
-(a²-2ab+b²)=4ab
ответ: надо прибавить учетверенное произведение этих чисел