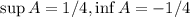Докажем вначале важное утверждение которым и воспользуемся.
Утверждение:
Пусть А - непустое и не конечное множество, так что . Предположим что существует так что . Если существует последовательность элементов из А выполняющая то .
Доказательство:
Допустим от противного, что , тогда существует так что .
Из-за того что , обязательно выполняется что противоречит тому что .
Следовательно .
Существует эквивалентное утверждение связанное с инфимумом, но доказывать его не буду (оно аналогично доказательству, но с некоторыми изменениями).
Теперь решим саму задачу:
Заметим что данное множество состоит из элементов последовательности , а также тот факт что для всех :
Скорость рабочих у нас определяется количеством сделанных деталей в час. Первый за время t делает делает на три детали больше, чем второй за тоже время. Например:
V1 * t = 4; V2 * t = 1.
Т.е. первый со своей скоростью за некоторое время t сделает четыре детали, когда второй со своей скоростью за тоже время сделает только 1-у деталь. Вычтем первое, как большее, из второго:
V1*t - V2*t = 3 t(V1 - V2) = 3 V1 - V2 = 3/t V1 = 3/t + V2 Поскольку скорость рассматривается за час времени, то V1 = V2 + 3
Едем дальше.
V1 * t = 352 V2 * (t + 6) = 418
Т.е. За некоторое время t первый делает 352 детали. Второй со своей скоростью за то же время и ещё шесть часов делает 418 деталей.
Для начала делим все произведение на COSx, при этом найдя ОДЗ для косинуса (Не равно нулю!). ОДЗ будет х не равно пи/2+пи*n, n принадлежит Z. Получим 4 + 3tg x - 10 tg^2(x) = 0 умножаем на (-1) 10tg^2 (x) - 3tgx - 4=0. Заменяем tg x = t. и решаем квадратное уравнение относительно t. 10t^2 - 3t - 4 = 0 t1 = (3-13)\ 20 = - 0.5 t2 = 0.8 подставляем полученные значения вместо tgx=t tgx= - 0.5 x = arctg (-0.5) + Пи*n, n принадлежит Z x = - arctg 0.5 = ПИ*n? n принадлежит Z tg x = 0.8 x = arctg 0.8 + Пи*n, n принадлежит Z
Докажем вначале важное утверждение которым и воспользуемся.
Утверждение:
Пусть А - непустое и не конечное множество, так что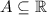 . Предположим что существует
. Предположим что существует 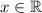 так что
так что 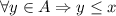 . Если существует последовательность
. Если существует последовательность 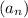 элементов из А выполняющая
элементов из А выполняющая 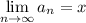 то
то 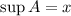 .
.
Доказательство:
Допустим от противного, что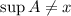 , тогда существует
, тогда существует 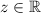 так что
так что 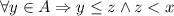 .
.
Из-за того что , обязательно выполняется
, обязательно выполняется 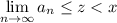 что противоречит тому что
что противоречит тому что 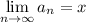 .
.
Следовательно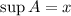 .
.
Существует эквивалентное утверждение связанное с инфимумом, но доказывать его не буду (оно аналогично доказательству, но с некоторыми изменениями).
Теперь решим саму задачу:
Заметим что данное множество состоит из элементов последовательности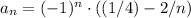 , а также тот факт что для всех
, а также тот факт что для всех 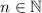 :
:
Т.е.:
Рассмотрим две подпоследовательности -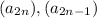
Так как:
Получаем: