Question

Найти все значения параметра а, при которых неравенство верно для любого х из отрезка: [-2; 2]: решить с пояснениями. ответ должен получиться такой:

Answer 1

$\dfrac{a(1-2a)+2ax}{2ax+2a^2-1}$

Рассмотрим функцию

$f(x)=1-\dfrac{4a^2-a-1}{2a^2+2ax-1}$

Она имеет разрыв при

$2a^2+2ax-1=0 \ \ \ \Rightarrow \ \ \ x=\dfrac{1-2a^2}{2a}$

"Вытолкнем" разрыв за пределы отрезка [-2; 2]

$\left[\begin{array}{I} \dfrac{1-2a^2}{2a}2 \end{array}} \ \Leftrightarrow \ \left[\begin{array}{I} \dfrac{2a^2-4a-1}{2a}0 \\ \dfrac{2a^2+4a-1}{2a}$

$a \in \left(- \infty; \ \dfrac{-2-\sqrt{6}}{2} \right) \cup \left( \dfrac{2- \sqrt{6}}{2}; \ 0 \right) \cup \left( 0; \ \dfrac{-2+ \sqrt{6}}{2} \right) \cup \left(\dfrac{2+\sqrt{6}}{2}; \ + \infty \right)$

получили ограничения по a.

Вернемся к функции. Заметим, что она монотонна ⇒ если f(-2)<0 и f(2)<0, то при любом x из отрезка [-2; 2] функция принимает отрицательные значения.

$\left\{\begin{array}{I} \dfrac{-2a^2-3a}{2a^2-4a-1}0 \end{array}} \ \Leftrightarrow \\$

$\Leftrightarrow \ \left\{\begin{array}{I} a \in (- \infty; \ -1,5) \cup \left( \dfrac{2- \sqrt{6}}{2}; \ 0 \right) \cup \left(\dfrac{2+ \sqrt{6}}{2}; \ + \infty \right) \\ a \in \left(- \infty; \ \dfrac{-2-\sqrt{6}}{2} \right) \cup \left(0; \ \dfrac{-2+ \sqrt{6}}{2} \right) \cup (2,5; \ + \infty) \end{array}}$

$a \in \left( - \infty; \ \dfrac{-2-\sqrt{6}}{2} \right) \cup (2,5; \ + \infty)$

Решение полностью попадает в ранее найденные ограничения.

ответ: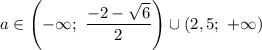 $a \in \left( - \infty; \ \dfrac{-2-\sqrt{6}}{2} \right) \cup (2,5; \ + \infty)$

________________________________________________________

$2a^2+4a-1=0\\ \frac{D}{4}=4+2=6\\ a=\dfrac{-2 \pm \sqrt{6}}{2}\\ \\ 2a^2-4a-1=0\\ \frac{D}{4}=4+2=6\\ a=\dfrac{2 \pm \sqrt{6}}{2}$