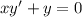
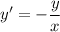 - уравнение с разделяющимися переменными
- уравнение с разделяющимися переменными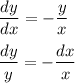
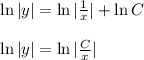
 - общее решение
- общее решение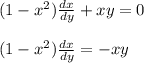

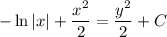 - общий интеграл
- общий интеграл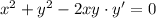

 , тогда
, тогда 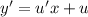



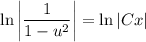
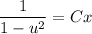
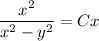 - общий интеграл
- общий интеграл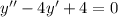
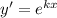 , тогда будем иметь характеристическое уравнение следующего вида:
, тогда будем иметь характеристическое уравнение следующего вида:
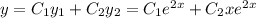 - общее решение
- общее решение
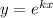 , тогда получаем
, тогда получаем
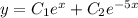

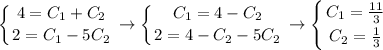
 - частное решение
- частное решение
Найти а) частное решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям ;
б) общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами .
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
a) y " + 8y ' + 7y = 0 ; y(0) = 2 ; y '(0) = 1 .
Составляем и решим характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
k² + 8k +7 =0 D₁ = (8/2)² - 7 = 4² -7 = 9 = 3² ; √D₁ =3
* * * очевидно по т Виета * * * k = - 1 корень
k₁,₂ = - (8/2) ± 3
k₁ = -4 - 3 = - 7 ;
k₂ = - 4 + 3 = -1 .
Получены два различных действительных корня
Общее решение : y = C₁e^(-7x) +C₂e^(-x) , где C₁ и C₂ произвольные константы (постоянные) .
* * * Придавая константам различные значения, можно получить бесконечно много частных решений * * *
Определим частное решение удовлетворяющее заданным начальным условиям : y(0) = 2 , y ' (0) = 1 .
y(0) = C₁e^(-7*0) +C₂e^(-0 ) = C₁ + C₂ = 2;
y ' = ( C₁e^(-7x) +C₂e^(-x) ) ' = -7*C₁e^(-7x) - C₂e^(-x)
y ' (0) = -7*C₁e^(-7*0) - C₂e^(-0) = - 7C₁ - C₂ = 1 .
- - - Составим и решим систему из двух найденных уравнений:
{ C₁ + C₂ = 2 ; {-6C₁ = 2+1 ; {C₁ = -0,5 ; { C₁ = - 0,5 ;
{ - 7C₁ - C₂ = 1 . { C₂ = - 7C₁ - 1. { C₂ =-7*(-0,5) -1 . { C₂ = 2,5 .
* * *методом сложения * * *
Подставим найденные значения C₁ и C₂ в общее решение
ответ : - 0,5 e^(-7x) +2,5 e^(-x) частное решение удовлетворяющее заданным начальным условиям.
- - - - - - -
б) y ' ' - 6y ' + 8y = 3e^ 4x
k² - 6k + 8 =0 ( характеристическое уравнение )
k₁ = 2 ;
k₂ = 4 .
y₀= C₁e^(2x) +C₂e^(4x) общее решение без правой части
Далее найдем частное решение данного уравнения по правой части у₁ =Axe^(4x) , у₁' = Ae^(4x) +4Axe^(4x) , у₁' ' = 4Ae^(4x) +4A(e^(4x) +4xe^(4x) )=8Ae^(4x) +16Axe^(4x)
8Ae^(4x) +16Axe^(4x) - 6Ae^(4x) -24Axe^(4x) +8Axe^(4x) =3e^4x
2Ae^(4x) =3e^(4x ) ⇒ A =1,5 ; y₁=Axe^(4x) = 1,5xe^(4x)
y = y₀ + y₁ = C₁e^(2x) +C₂e^(4x)+ 1,5xe^(4x)
ответ : C₁e^(2x) +C₂e^(4x)+ 1,5xe^(4x) .
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
ay ' ' + by' + cy =0 ищем решение y= е^(kx) || ^ → степень ||
y ' = е^(kx) *(kx) ' =k*е^(kx) ; y '' =(y ' )'= (k*е^(kx) ) '=k*(е^(kx) ) '= k²*е^(kx) .
a*k²*е^(kx) + b*k*e^(kx)+c*e^(kx) =0 ;
е^(kx) * (ak² + bk +c) =0 ; е^(kx) ≠ 0 ⇒
a*k² + b*k + c = 0 ( характеристическое уравнение )
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

в задании 2г пропущен показатель степени n, а в заданиях 1с и 2з - лишние показатели - вынуждена придумать сама и удалить.
1. а) 16m⁶y² - 9m⁴ = (4m³y)² - (3m²)² = (4m³y - 3m²)(4m³y + 3m²)
b) 9x⁸y⁴ - 100z² = (3x⁴y²)² - (10z)² = (3x⁴y² - 10z)(3x⁴y² + 10z)
c) 0,81p⁶q⁴ - 0,01x² = (0,9p³q²)² - (0,1x)² = (0,9p³q² - 0,1x)(0,9p³q² + 0,1x)
2.
a) 64 - y⁴ = 8² - (y²)² = (8 - y²)(8 + y²)
б) x² - c⁶ = х² - (с³)² = (х - с³)(х + с³)
в) a⁴ - b⁸ = (а²)² - (b⁴)² = (a² - b⁴)(a² + b⁴) = (a - b²)(a + b²)(a² + b⁴)
г) 25m⁶ - n² = (5m³)² - n² = (5m³ - n)(5m³ + n)
д) 1 - 49p¹⁰ = 1² - (7p⁵)² = (1 - 7p⁵)(1 + 7p⁵)
е) 4y⁶ - 9a⁴ = (2y³)² - (3a²)² = (2y³ - 3a²)(2y³ + 3a²)
ё) 64 - a⁴b⁴ = 8² - (a²b²)² = (8 - a²b²)(8 + a²b²)
ж) 16b²c¹² - 0,25 = (4bc⁶)² - (0,5)² = (4bc⁶ - 0,5)(4bc⁶ + 0,5)
з) 81x⁶y² - 0,36a² = (9x³y)² - (0,6a)² = (9x³y - 0,6a)(9x³y + 0,6a)