Задание № 1:
Найдите последнюю ненулевую цифру значения произведения 40^50*50^40?
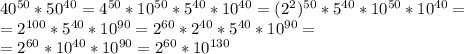
10^130 нас не интересует. Попробуем повозводить 2 в степень:
2^1=2, 2^2=4, 2^3=8, 2^4=16, 2^5=32
Пятая степень, как и первая, оканчивается на 2. Образуется своего рода цикл.
Чтобы узнать последнюю цифру степени N, нужно N разделить на 4. Остаток от деления соответствует степени, последняя цифра которой совпадает с последней цифрой степени N. Остаток 0 соответствует 4-ой степени.
60/4=15, остаток 0 – 4 степень оканчивается на 6, значит и 60 степень оканчивается на 6
ОТВЕТ: 6
Задание № 3:
Сколько корней имеет уравнение: |x|=|x−1|+x−3?
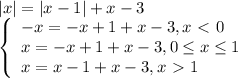
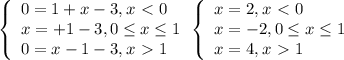
Условию раскрытия модуля соответствует только третья строчка.
ОТВЕТ: 1
Разложите на множителе трехчлен ₁ ₂
1) x² - 2x + 12 ;
2) x ² + x + 20 .
Объяснение: i² = -1
1) x ² - 2x + 12 D₁ = D/4 = (-2/2)² - 12 = (-1)² -12 = -11 < 0 значит корни квадратного трехчлена комплексные. [ i = √ (-1) → мнимая единица ]
x₁ = 1 -√11 i, x₂ = 1 +i√11 i
* * *x₁+x₂ =2 ; x₁*x₂=( 1 -√11 i)(1 +√11 i) =1² -(11 i)²=1-11i²=1-11*(-1) =1+11 =12 * * *
x²- 2x + 12 = (x -x₁)*(x-x₂) =(x - 1 -(√11) i )*(x - 1 +(√11) i )
z = a+bi ; |z| =r = √(a²+b²) → модуль комплексного числа
a =r(cosφ+ i*sinφ) φ _ аргумент комплексного числа tgφ =b/a
25+80m+64m² наверное?