1. Обозначим ширину бассейна через X. Тогда его длина будет равна X + 6.
2. Площадь бассейна равна произведению длины на ширину. То есть: S1 = X * (X + 6).
3. Определим площадь бассейна с учетом ширины дорожки. Стороны прямоугольника с учетом дорожки равны: ширина - X + 0,5, длина X + 6,5. Тогда площадь S2 = (X + 0,5) * (X + 6,5).
4. По условию задачи площадь дорожки 15 м^2. То есть, S2 - S1 = 15.
5. Получили уравнение задачи: (X + 0,5) * (X + 6,5) - X * (X + 6) = 15.
6. Упростим выражение. Получим: X = 15 - 6,5 * 0,5 = 11,75 м.
7. Длина бассейна равна: X + 6 = 17,75 м.
ответ: ширина бассейна 11,75 м, длина 17,75 м.
a) t₁ = 0.6 c; б) h max = 3.2 м; в) t₂ = 1.4 c.
Объяснение:
у₀ = 1.4 м - начальная координата мяча
v₀ = 6 м/с - начальная скорость мяча
g = 10 м/с² - ускорение свободного падения
Координата мяча при движении формулой
у = у₀ + v₀t - 0.5gt² -уравнение движения
у = 1,4 + 6t - 5t² (м) (1) - зависимость координаты мяча от времени
v = v₀ - gt -уравнение для скорости
v = 6 - 10t (м/с) (2) - зависимость скорости мяча от времени
a) В момент t₁, когда мяч достигнет максимальной высоты, его скорость станет равной нулю
Из формулы (2) получим 0 = 6 - 10t₁ ⇒ t₁ = 0.6 (c)
б) Подставим значение t₁ = 0,6с в формулу (1) и найдём h max
h max = 1.4 + 6 · 0.6 - 5 · 0.6² = 3.2 (м)
в) В момент t₂ падения мяча на землю его координата будет равна нулю. Подставим в формулу (1) значение у = 0
0 = 1,4 + 6t - 5t²
5t² - 6t - 1.4 = 0
D = 6² + 4 · 5 · 1.4 = 64
√D = 8
t₁ = (6 - 8)/10 = -0.2 - не подходит по физическому смыслу времени
t₂ = (6 + 8)/10 = 1.4 (c)
2/3+3=3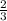
0,02+3/4=0,75+0,02=0,77