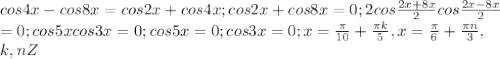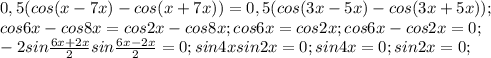;
;
;
. 
Здесь получается интересно, так как все решения уравнения 
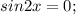входят в решения уравнения 
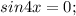к слову, это что-то типа тривиальных систем/совокупностей, уже всё доказано, нам этого делать не обязательно, хотя можно изобразить все решения одного и второго ур-я и проверить, это так, к слову. 
. 
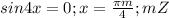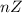и всё подобное означает, что n принадлежит множеству целых чисел, просто я не нашёл значка принадлежности в редакторе формул/уравнений на этом сайте.
2)196/70
3.)3,2