Задание решается методом интервалов:
1. (х² - 11)(15 - х²) ≥ 0
1) Находим нули
(х² - 11)(15 - х²) = 0
если
х = ±√15
х = ±√11
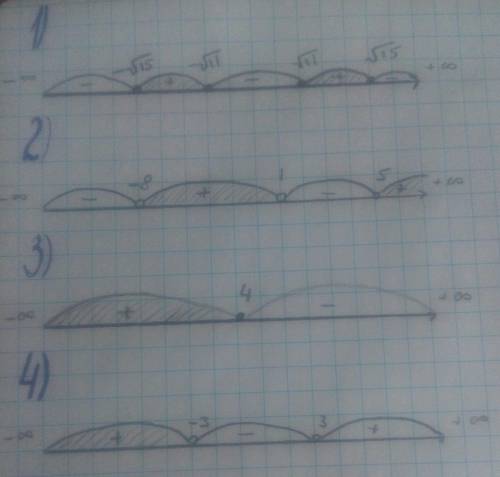
2) Отмечаем корни на координатной прямой (см. приложение)
Черными точками обозначаются числа, включающиеся в интервал, а белыми — исключающиеся из него.
3) Отмечаем знаки функций на координатной прямой (см. приложение)
Определяются методом подстановки чисел из интервала.
ответ: х ∍ [-√15;-√11] U [√11;√15]
Квадратные скобки говорят, что числа в них включаются в интервал, а круглые, что числа исключаются из него.
Остальное решается аналогично.
2. (х² - 6х + 5)(х + 8) > 0
(х² - 6х + 5)(х + 8) = 0
если
х = -8
…………………………(х² - 6х + 5)
…………………………D = 16
х = 5
х = 1
ответ: х ∍ (-8;1) U (5;+∞)
3. (х² - х + 11)(4 - х) ≥ 0
(х² - х + 11)(4 - х) = 0
если
х = 4
…………………………(х² - х + 11)
…………………………D = -43; D < 0
…………………………ветви параболы направлены вверх.
…………………………функция всегда положительная
ответ: х ∍ (-∞;4]
4. (х² + 2х + 14)(х² - 9) > 0
(х² + 2х + 14)(х² - 9) = 0
если
х = ±3
……………………………(х² + 2х + 14)
……………………………D = -52; D < 0
……………………………ветви параболы направлены вверх
……………………………функция всегда положительная
ответ: х ∍ (-∞;-3) U (3;+∞)
Пусть одна из сторон образовавшегося прямоугольника равна х см, то другая - (24-х) см. Площадь прямоугольника вычисляются по формуле S=a*b, то S=x*(24-x)
Зададим функцию S(x)=x*(24-x), исследуем ее и найдем при каком значении она принимает наибольшее значение. S(x)=x*(24-x)=24x-x^2
D(S)=(0; 24)
S'(x)=24-2x
S'(x)=0, 24-2x=0
-2x=-24
x=12
Найдем значение производной данной функции слева S'(11)=2>0 и справа S'(13)=-2<0 от значения х=12. Значение производной меняется с + на -, значит функция в точке х=12 достигает своего максимума. Площадь прямоугольника будет наибольшей, если стороны его 12см и 12 см, т.е - квадрат
ответ: 0.56