1) Імовірність випадення числа меншого від 5 = 4/6=2/3, бо числа 1 2 3 4 задовольняют умову, а всього на кубику 6 чисел.
Імовірність випадення числа більшого за 4 = 2/6=1/3, бо числа 5 6 задовольняють умову, а всього на кубику 6 чисел.
Для отримання результату помножимо ймовірність виконання умови при першому кидку на ймовірність виконання умови при другому кидку: 2/3*1/3=2/9
2)Імовірність виконнная умови 5/6 при першому кидку і 1/6 при другому. Отримуємо 1/6*5/6=5/36
3)Імовірність випадення на кубику при першому киданні числа більшого ніж при другому киданні дорівнює 1/2-1/6=1/3, оскільки 1/6-імовірність випадення дубля. Наприклад, перший раз випало число 1. Імовірність випадення того самого числа при другому киданні дорівнює 1/6 (6 варіантів 1 з яких нас задовольняє).1/2 ми вказуємо, бо при киданні використовується один і той самий кубик, і кількість випадків, які нас задовольняють удвічі менша за тотальну кількість імовірних подій, тобто імовірність симетрична.
Отже, відповідь: 1/3
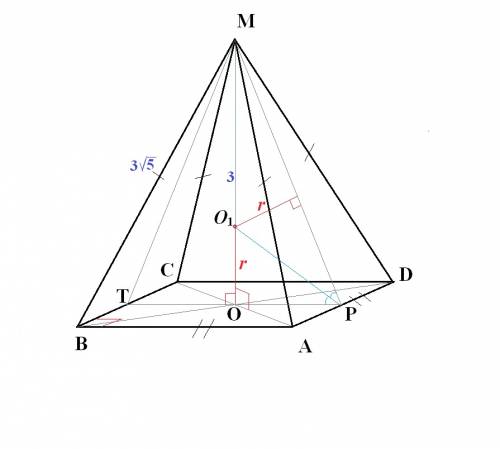
Чертеж во вложении.
Пирамида МАБСД. МО=3 -высота, МВ=МА=МС=МД=3√5.
О₁ - центр вписанной сферы.
АВСД - квадрат, О-центр вписанной и описанной окружностей.
∆ВМО-прямоугольный. По теореме Пифагора
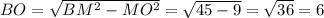
∆ВОA-прямоугольный, ОВ=ОА. По теореме Пифагора
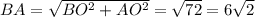
Тогда ОР=1/2АВ=3√2.
В прямоугольном ∆МОР по теореме Пифагора
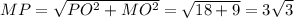
О₁ - центр вписанной сферы, является центром вписанной в ∆ТМР окружности. Для этой окружности и для сферы r=ОО₁.
Тогда О₁ - точка пересечения биссектрис ∆ТМР.
Рассмотрим прямоугольный ∆МОР. РО₁-биссектриса. МО₁=МО-ОО₁=3-r.
По свойству биссектрисы треугольника
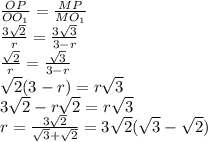
Площадь сферы:
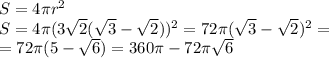
3a²(1+2b⁴) После 6а² умножить же?