Алгебра: (6,3+3*(35 17/42-6 6/35))*(0,7-1/12)*6

(6,3+3(35 17/42-6 6/35))(0,7-1/12)*6

👇

Ответ:

scrubble

08.08.2021

6 : 3 + 3 * ( 35 17/42 - 4 6/25)) * ( 0,7 - 1/12) * 6=354 759/3500
1) 6:3=2
2) 35 17/42 - 4 6/25=35 425/1050-4 168/1050=31 257/1050
3) 3*31 257/1050=3*32807/1050=32807/350=93 257/350
4) 2+ 93 257/350=95 257/350=33507/350
5) 0,7-1/12=7/10-1/12=42/60-5/60=37/60
6) 37/60* 33507/350=1239759/21000
7) 1239759/21000*6=1239759/3500=354 759/3500

4,4(40 оценок)

Открыть все ответы

Ответ:

sluvka123123

08.08.2021

1. Область определения функции: множество всех действительных чисел

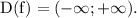
$\mathrm{D(f)=(-\infty;+\infty).}$

2. Чётность и нечётность функции: проверим на четность функции с соотношений: 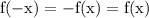$\mathrm{f(-x)=-f(x)=f(x)}$

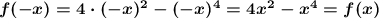
$\boldsymbol{f(-x)=4\cdot(-x)^2-(-x)^4=4x^2-x^4=f(x)}$

Итак, f(-x) = f(x) значит заданная функция является четной.

3. Точки пересечения с осями координат.

3.1. точки пересечения с осью Ох. График функции пересекает ось абсциссу при f = 0 значит нужно решить уравнение:

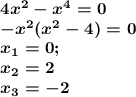
$\boldsymbol{4x^2-x^4=0}\\ \boldsymbol{-x^2(x^2-4)=0}\\ \boldsymbol{x_1=0;}\\ \boldsymbol{x_2=2}\\ \boldsymbol{x_3=-2}$

(0;0), (2;0), (-2;0) - точки.

3.2. точки пересечения с осью Оу. График пересекает ось ординат, когда х=0, т.е. подставляем x=0 в функцию, получим

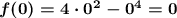
$\boldsymbol{f(0)=4\cdot0^2-0^4=0}$

(0;0) - точка

4. Функция не является периодичной.

5. Экстремумы функции

Для того, чтобы найти экстремумы, нужно решить уравнение 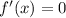f'(x)=0

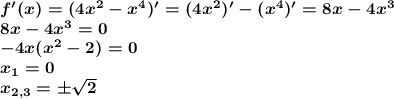
$\boldsymbol{f'(x)=(4x^2-x^4)'=(4x^2)'-(x^4)'=8x-4x^3}\\\boldsymbol{8x-4x^3=0}\\ \boldsymbol{-4x(x^2-2)=0}\\ \boldsymbol{x_1=0}\\ \boldsymbol{x_{2,3}=\pm\sqrt{2}}$

Найдем интервалы возрастание и убывания функции:

______+____(-√2)_____-____(0)________+_____(√2)______-____

Функция возрастает на промежутке 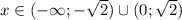$x \in (-\infty;-\sqrt{2})\cup(0;\sqrt{2} )$ , а убывает -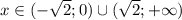 $x \in (-\sqrt{2};0 )\cup(\sqrt{2} ;+\infty)$

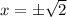$x=\pm\sqrt{2}$ - локальные максимумы

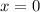x=0 - локальный минимум.

6. Точки перегиба.

Вторая производная функции: 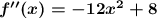$\boldsymbol{f''(x)=-12x^2+8}$

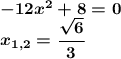
$\boldsymbol{-12x^2+8=0}\\ \boldsymbol{x_{1,2}=\dfrac{\sqrt{6} }{3}}$

___-____(-√6/3)____+__(√6/3)___-____

Функция вогнутая на промежутке 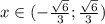$x \in (-\frac{\sqrt{6} }{3} ;\frac{\sqrt{6} }{3} )$ , а выпуклая на промежутке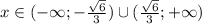 $x \in (-\infty;-\frac{\sqrt{6} }{3} )\cup(\frac{\sqrt{6} }{3} ;+\infty)$

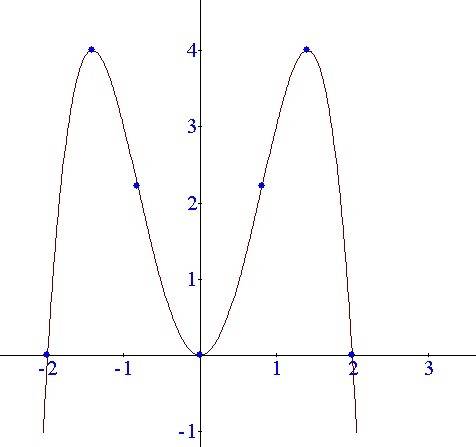
7. Асимптоты

Здесь вертикальных асимптот нет. Найдем теперь горизонтальные асимптоты.

Горизонтальные асимптоты найдём с пределов данной функции при 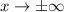$x\to \pm\infty$

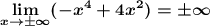
$\displaystyle \boldsymbol{ \lim_{x \to \pm\infty} (-x^4+4x^2)=\pm\infty}$

Предел не существует, следовательно горизонтальной асимптоты нет.

Вертикальной асимптоты нет.

4x^2-x^4 исследовать и построить график функции.

4,5(90 оценок)

Ответ:

Диля222222222

08.08.2021

А) объединяем y>x-3 и y≤-x+3 получаем x-3<y≤-x+3
это возможно когда x-3<-x+3
2x<6
x<3
ответ: x-3<y≤-x+3 при x<3

b) x-2y<4 и x+y<3 ⇒ x<4+2y и x<3-y
найдем что меньше 4+2y или 3-y
1) допустим 4+2y < 3-y, тогда 2y+y < 3-4
3y < -1
y<-1/3
x<4+2y при y<-1/3
2) теперь допустим наоборот 4+2y > 3-y
y>-1/3
x<3-y при y>-1/3
ответ:x<4+2y при y<-1/3 и x<3-y при y>-1/3

с) -2x+y<-1 и x-y>3
y+1<2х и x-3>y
y<2х-1 и x-3>y
y<2х-1 и y<x-3
1) пусть 2х-1<x-3
x<-2
ответ: y<2х-1 при x<-2 и y<x-3 при x>-2

d) x+y>=3 и x-y<2

x≥3-y и x<2+y
3-y≤x<2+y
Это возможно при 3-y<2+y
1<2y
y>1/2
ответ: 3-y≤x<2+y при y>1/2

4,5(50 оценок)

Это интересно:

Компьютеры-и-электроника

10.04.2020

Как победить Элитную Четверку в Pokemon FireRed...

22.05.2023

Как убедить родителей не пустить вас в школу: советы для тех, кто хочет изменить свою жизнь...

Хобби-и-рукоделие

04.09.2020

Как сделать фетровую шляпу: пошаговая инструкция с фото...

Хобби-и-рукоделие

01.08.2021