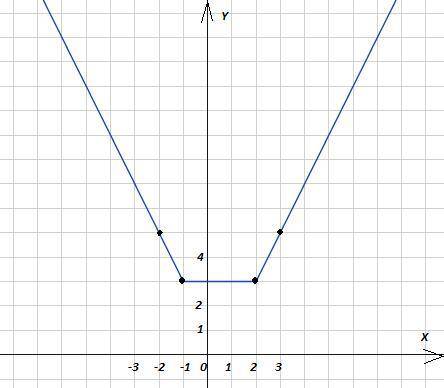
y = |x - 2| + |x + 1|
Нужно найти точки, в которых выражения под модулем меняют знак.
x - 2 = 0; x₁ = 2; x + 1 = 0; x₂ = -1
Эти точки разбивают числовую прямую на три интервала.
1) x ∈ (-∞; -1]
y = |x - 2| + |x + 1| = -x + 2 - x - 1 = -2x + 1;
y = -2x + 1 - линейная функция. Точки для построения
x₁ = -2; y₁ = 5; x₂ = -1; y₂ = 3
2) x ∈ (-1; 2)
y = |x - 2| + |x + 1| = -x + 2 + x + 1 = 3;
y = 3 - линейная функция. График - прямая, параллельная OX
3) x ∈ [ 2; +∞)
y = |x - 2| + |x + 1| = x - 2 + x + 1 = 2x - 1;
y = 2x - 1 - линейная функция. Точки для построения
x₁ = 2; y₁ = 3; x₂ = 3; y₂ = 5
y(y-7)=8
y²-7y-8=0
D=49+32=81
y₁= 7-9 = -1
2
y₂= 7+9 =8
2
При у= -1
х² -2х= -1
х² -2х+1=0
(х-1)² =0
х=1
При у=8
x² -2x=8
x² -2x-8=0
D=4+32=36
x₁= 2-6 = -2
2
x₂= 2+6 = 4
2
ответ: -2; 1; 4