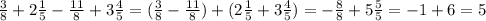
(3/8-11/8)+(2 1/5+3 4/5)= -1+6=5. ответ : 5.
1. За 1 - принимается весь объем работы.
Пусть X - время, которое на перепечатку рукописи затрачивает первая машинистка.
Тогда 1/ X - ее производительность.
(X - 2) - время, которое на перепечатку рукописи затрачивает вторая машинистка.
И 1/(X - 2) - ее производительность.
2. Запишем выражение для производительности совместной работы.
2 часа 24 минуты = 2 часа + 24/60 часа = 2,4 часа.
1/ X + 1 / (X - 2) = 2,4.
Решаем уравнение приведением к общему знаменателю.
X - 2 + X = 2,4 * X * X - 4,8 * X.
2,4 * X * X - 6,8 * X + 2 = 0.
3. Решаем квадратное уравнение через дискриминант.
D = 6,8 * 6,8 - 2.4 * 2 * 4 = 46,24 - 19,2 = 27,04
X1 = (6,8 + 5,2) / 4,8 = 12 / 4,8 = 2,5 часа = 2 часа 30 минут- время первой машинистки.
2,5 - 2 = 0,5 = 30 минут - время второй машинистки.
X2 = (6,8 - 5,2) / 4,8 = 1,6 / 4,8 = 1/3 часа.
(1 / 3 - 2) - величина отрицательная, этого быть не может.
Значит в задаче только одно решение.
ответ: Для перепечатки рукописи первой машинистке нужно 2 часа 30 минут, а второй - 30 минут.
Объяснение:
Объяснение:
((a+7)\(a-7)-(a-7)\(a+7))\(14\(a^2-7a))
Приведем дроби в скобке к общему знаменателю a^2-49, домножив первую дробь на (a+7), а вторую на (a-7):
((a+7)^2-(a-7)^2)\(a^2-49)
По формуле разности квадратов:
((a+7-a+7)(a+7+a-7))\(a^2-49)
14*2a\a^2-49
28a\a^2-49
Представим деление одной дроби на другую умножением первой на перевернутую вторую:
(28a*(a^2-7a))\(14*(a^-49))
Вынесем в числителе "а" за скобку, а в знаменателе разложим скобку на множители:
(28a^2*(a-7))\(14(a-7)(a+7))
Сократим дробь:
2a^2\(x+7)