Применим формулу сокращённого умножения:
a² - b² = (a - b)·(a + b).
1) 9·x²-4·y²-3·x+2·y = (3·x)²-(2·y)²-(3·x-2·y) = (3·x-2·y)·(3·x+2·y) - (3·x-2·y) =
= (3·x-2·y)·(3·x+2·y-1);
2) 81 - (3-8·y)² = 9² - (3-8·y)² = (9-(3-8·y))·(9+(3-8·y)) = (9-3+8·y)·(9+3-8·y) =
= (6+8·y)·(12-8·y) = 2·(3+4·y)·4·(3-2·y) = 8·(3+4·y)·(3-2·y);
3) 36-(y+1)² = 6²-(y+1)² = (6-(y+1))·(6+(y+1)) = (6-y-1)·(6+y+1) = (5-y)·(7+y);
4) (4-5·x)²-64 = (4-5·x)²-8² = (4-5·x-8)·(4-5·x+8) = (-4-5·x)·(12-5·x) =
= -(4+5·x)·(12-5·x) = (4+5·x)·(5·x-12).
Пусть гусеничный трактор вспахивает х га в день. Тогда два гусеничных трактора вспашут 2х га в день.
Пусть один колесный трактор вспахивает у га в день.
Вместе два гусеничных и один колесный тракторы вспахали 22 га.
Составим уравнение: 2х+у=22
Во второй день три гусеничных трактора вспахали 3х га, а восемь колесных тракторов вспахали 8у га. Вместе все они вспахали 72 га.
Составим уравнение: 3х+8у=72
Получаем систему уравнений:
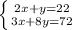
Из первого уравнения выразим у и подставим во второе уравнение. Тем самым найдем х.
2х+у=22
у=22-2х
Подставляем: 3х+8(22-2х)=72
3х+176-16х=72
176-72=16х-3х
104=13х
х=104:13
х=8 (один гусеничный трактор в день обрабатывал 8 га земли)
Полученный результат подставим в первое уравнение и найдем чему равен у, т.е. сколько га земли обрабатывает в день колесный трактор.
2*8+у=22
у=22-2*8
у=22-16
у=6 (один колесный трактор в день обрабатывает 6 га земли)
ответ: 8 га земли обрабатывает в день гусеничный трактор, 6 га земли обрабатывает в день колесный трактор.
Вот графическое решение