* * * * * * * * * * * * * * * * * * * * * * * * *
Решите систему уравнений { 3xy -x =5 ; 3xy -y= 4
ответ: (x₁ ; y₁) = ( -5/3 ; -2/3 ) ; ( x₂ ; y₂) = (1 ; 2) .
Объяснение:
{ 3xy -x =5 ; 3xy -y= 4 . ⇔ { 3xy -x-(3xy -y) = 5 - 4 ; 3xy -x =5 . ⇔
{ y=x+1 ; 3xy - x =5 .⇔ { y=x+1 ; 3x(x+1) - x -5 =0 .⇔ { y=x+1 ; 3x²+2x -5 =0 .
3x²+2x -5 =0
D₁= D/4 =( 2/2)² - 3*(-5) =1²+15 =16 = 4² ; x = (-1 ± √D₁)/3
⇒ x₁ = (-1 -4) /3 = - 5/3 ⇒ y₁ = x₁+1 = -5/3+1 = -2/3
x₂ = (-1 +4) /3 = 1 ⇒ y₂ = x₂+1 =1 +1 = 2 .
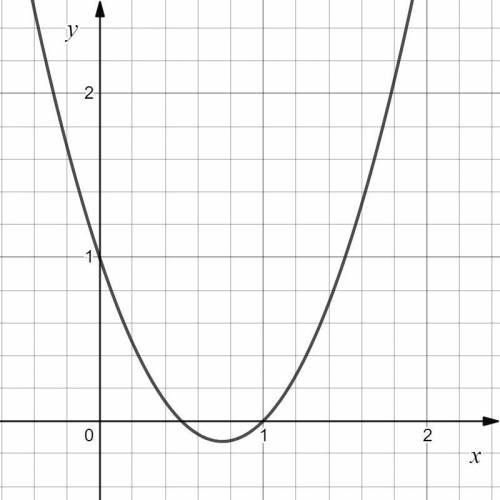
— квадратичная функция, график которой — парабола с ветвями, направленными вверх.
Нули функции:
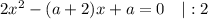
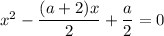
Согласно теореме Виета, имеем:
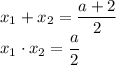
По условию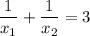 
или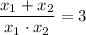 
.
Следовательно, подставляя значения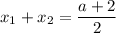 
и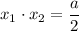 
, найдем параметр 
:
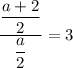
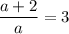
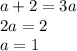
Таким образом,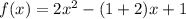 
, то есть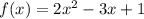 
Найдем координаты точки вершины параболы:
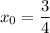
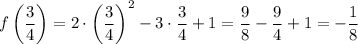
Значит,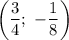 
— точка вершины параболы.
Найдем точки пересечения с осями координат:
а) С осью абсцисс:
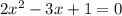
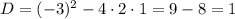
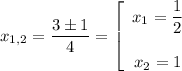
Следовательно,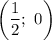 
и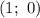 
— точки пересечения функции с осью абсцисс.
б) С осью ординат:
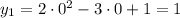
Следовательно,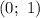 
— точка пересечения с осью ординат.
Согласно свойству симметрии параболы,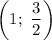 
— точка графика.
Изобразим график данной функции (см. вложение).
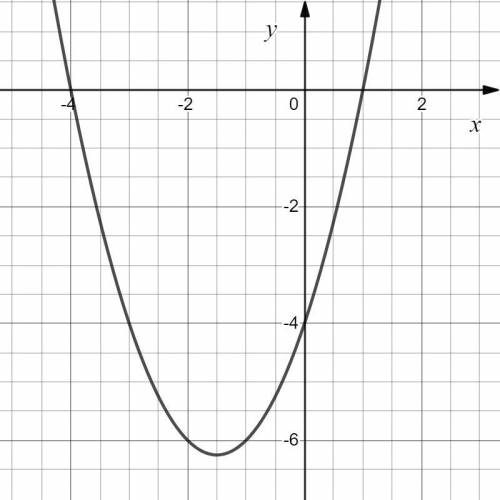
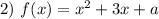— квадратичная функция, график которой — парабола с ветвями, направленными вверх.
Нули функции:
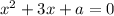
Согласно теореме Виета, имеем:
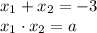
По условию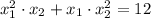 
Следовательно, подставляя значения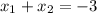 
и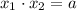 
, найдем параметр :
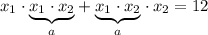
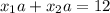
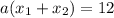
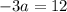
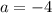
Таким образом,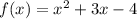 
Найдем координаты точки вершины параболы:
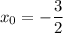
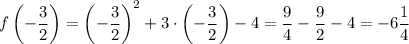
Найдем точки пересечения с осями координат:
а) С осью абсцисс:
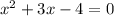
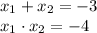
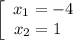
Следовательно,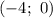 
и 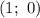— точки пересечения функции с осью абсцисс.
б) С осью ординат:
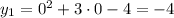
Следовательно,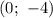 
— точка пересечения с осью ординат.
Согласно свойству симметрии параболы,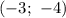 
— точка графика.
Изобразим график данной функции (см. вложение).
