Подробное объяснение: в задании номер 1 число 3 в 4 степени возводится в 5 степень. Когда ты видишь что-то наподобие этого, то степени перемножаются: то есть 4 степень умножаем на 5 степень и получаем 20 степень, то есть 3 в 20 степени. Далее, в числителе, видим:
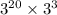
Здесь степени тоже умножаюся, потому что умножаются сами числа. Перемножаем и получаем 3 в 23 степени. Ну и затем остается сократить то, что получилось:
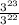
Сокращаем и получаем:
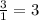
Задание номер 2.
Ну, тут все просто, тут надо правильно перемножить, как на фото. С умножением степеней ситуация та же, что и в 1 задании.
Надеюсь
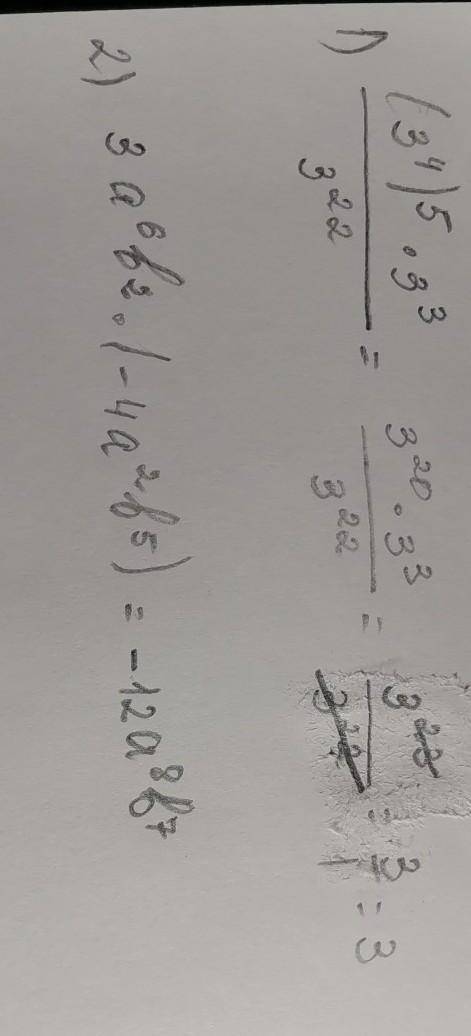
прощения, что не в рукописном варианте, но думаю, что ход мыслей будет понятен=)
Нужно помнить, про то, что значение x, стоящего под логарифмом - всегда строго больше нуля (ОДЗ: 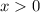 ).
).
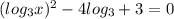
Пусть 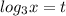 , тогда:
, тогда:
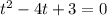
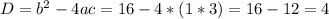
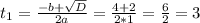
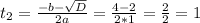
Тогда:
1). 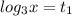
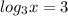 (теперь нужно представить 3 так, чтобы под логарифмом было такое число, которое с основанием логарифма
(теперь нужно представить 3 так, чтобы под логарифмом было такое число, которое с основанием логарифма 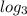 будет равняться 3 (иначе говоря 3 в степени 3 (первая 3 - для того, чтобы сократить
будет равняться 3 (иначе говоря 3 в степени 3 (первая 3 - для того, чтобы сократить 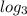 и после этого осталась чистая степень - 3)
и после этого осталась чистая степень - 3)
(таким числом под логарифмом будет 27: 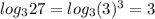 )
)
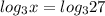 (одинаковые логарифмы с основанием 3>1 - можем их убрать)
(одинаковые логарифмы с основанием 3>1 - можем их убрать)
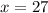
2). 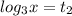
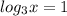 (сделаем тоже самое: нужно представить 1 так, чтобы под логарифмом было такое число, которое с основанием логарифма
(сделаем тоже самое: нужно представить 1 так, чтобы под логарифмом было такое число, которое с основанием логарифма 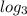 будет равняться 1 (иначе говоря 3 в степени 1 (3 - для того, чтобы сократить
будет равняться 1 (иначе говоря 3 в степени 1 (3 - для того, чтобы сократить 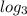 и после этого осталась чистая степень - 1))
и после этого осталась чистая степень - 1))
(таким числом под логарифмом будет 3: 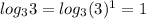 )
)
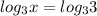 (одинаковые логарифмы с основанием 3>1 - можем их убрать)
(одинаковые логарифмы с основанием 3>1 - можем их убрать)
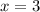
ответ: 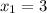 ,
, 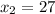
Здесь неопределённость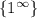 поэтому будем пользоваться вторым замечательным пределом
поэтому будем пользоваться вторым замечательным пределом