Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру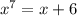 
уравнение в действительных корнях.
Рассмотрим функцию 
. Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию 
. Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение 
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
Пусть за х дней второй рабочий может один выполнить всю работу
х+4 дня нужно первому рабочему, чтобы выполнить всю работу
примем всю работу за 1 часть
7/ (х+4) часть работы выполнил первый рабочий за 7 часов
7-2 =5 часов работал второй рабочий
5/х часть работы выполнил второй рабочий за 5 часов
так как они выполнили всю работу, то
7/ (х+4) +5/х =1 или
х² -8х -20 =0 или
х= 10 или х= -2 ( посторонний корень)
ответ
10+4 =14 дней нужно первому рабочему, чтобы выполнить всю работу одному
10 дней нужно второму рабочему, чтобы выполнить всю работу одному
Так как точка перемещается вверх и вниз, будет меняться только координата Y.
1)-1-3=-4
2)-4+3=-1
3)-1+4,3=3,3
4)3,3-7,5=-4,2.
Координаты точки В2(-2;-4,2).