5 км/ч
Объяснение:
1) Пусть х - скорость течения реки, тогда
10 / (15 - х) - время движения туриста на катере;
10/х - время движения на плоту, так как скорость движения плота равна скорости течения реки.
2) Составим уравнение и найдём х:
10/х - 10 / (15 - х) = 1
10 · (15-х) - 10 · х = 15х - х²
(привели левую часть к общему знаменателю х·(15-х); слева домножили дроби и алгебраически их сложили, а затем левую и правую части умножили на х·(15-х); таким образом мы слева - освободились от знаменателя, а справа - получили 15х - х²).
150 - 10х - 10х = 15х - х²
х² - 10х - 10х - 15х +150 = 0
х² - 35х + 150 = 0
(так как коэффициент а перед х ² равен 1, то корни находим по формуле приведённого квадратного уравнения: х₁,₂ = половине второго коэффициента, взятого с противоположным знаком, ± корень квадратный из квадрата этой половины без свободного члена)
х₁,₂ = 17,5 ± √(17,5²-150) = 17,5 ±√(306,25-150) = 17,5 ±√156,25 = 17,5 ±12,5
х₁ = 17,5 - 12,5 = 5 км/ч
х₂ = 17,5 + 12,5 = 30 км/ч - этот корень отбрасываем, т.к. скорость течения реки не может быть больше скорости катера, иначе бы при движении против течения реки он бы двигался назад, а не вперёд.
ответ: скорость течения реки 5 км/ч
1) 1/6
2) 2sin(π/4 + a/2)cos(π/4 - a/2)
Объяснение:
1)
Событие A: "4 выбранных велосипеда из 10 не имеют дефектов"
Велосипеды по условию неразличимы, а порядок их выбора несущественен, поэтому для подсчета всевозможных и благоприятных событий воспользуемся конфигурацией сочетания.
Количество всех возможных событий:
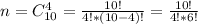
именно столько наборов из 4 велосипедов можно составить, имея в наличии все 10 штук
Количество благоприятных событий:
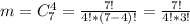
именно столько наборов из 4 велосипедов можно составить, располагая только 7 исправными (нам важно, чтобы все 4 выбранные велосипеда не имели дефектов)
Вероятность события A:
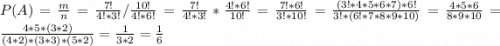
2)
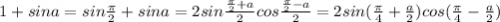
Следуя правилу комбинаторике, знаем, что
Из 3 цифр можно составить только 6 чисел
Т.е 3*2*1=6
По принципу построим математическую модель задачи,
7 8 9
8 9 7 9 8 7
9 8 9 7 7 8
Т.е 6 вариантов
ответ: 6