В решении.
Объяснение:
Розвяжіть нерівність:
а) x²-x-12<= 0.
Приравнять к нулю и решить как квадратное уравнение:
x²-x-12=0
D=b²-4ac = 1 + 48 = 49 √D= 7
х₁=(-b-√D)/2a
х₁=(1-7)/2
х₁= -6/2
х₁= -3;
х₂=(-b+√D)/2a
х₂=(1+7)/2
х₂=8/2
х₂=4.
Теперь начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -3 и х= 4, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у <= 0 (график ниже оси Ох) при х∈[-3; 4].
Решение неравенства х∈[-3; 4].
Неравенство нестрогое, скобки квадратные.
b) x² - 16 < 0
Приравнять к нулю и решить как квадратное уравнение:
x² - 16 = 0
x² = 16
х = ±√16
х = ±4.
Теперь начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -4 и х= 4, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у < 0 (график ниже оси Ох) при х∈(-4; 4).
Решение неравенства х∈(-4; 4).
Неравенство строгое, скобки круглые.
Відповідь:
1.
f(2)=8
f(-1)= - 2,5
нулі: f(0)=0
2. D(f): x ∈ (-∞;4)∪(4;6)∪(6;+∞)
3) в завданні
5)х ∈ [-5;-4) ∪(-4;4) ∪(4;+∞)
6)p=8 q=22
Пояснення:
1)f(2)=1/2*2²+3*2=2+6=8;
f(-1)=1/2*(-1)²+3*(-1)=0,5-3=-2,5
нулі х=0; f(0)=1/2*0+3*0=0 (при у=0 х=0)
2.область визначення функції: оскільки це дріб, то знаменник не може бути рівний 0
х²-10х+24≠0 D=(-10)²-4*1*24=100-96=4
x₁≠(10-2)/2≠4
x²≠(10+2)/2=6
Відповідь: D(f): x ∈ (-∞;4)∪(4;6)∪(6;+∞)
3. Побудувати графік функції:
це парабола , вітки направлені догори
Знайдемо точки перетину з вісью ОХ
x²+2x-3=0 по теоремі Вієта х1= - 3 , x2= 1.
координати вершини: хв=-2/2=-1, ув=(-1)²+2*(-1)-3=-4 (-1;-4)
при х=0, у=-3
графік перемалюєш з картинки
1)f(x)>0 при х ∈ (-∞; -3) ∪ (1;+∞)
f(x)<0 при х ∈ (-3; 1)
2)Е(f) : y ∈ (-5;+∞)
3) функція зростає при х ∈ [-1; +∞)
4.
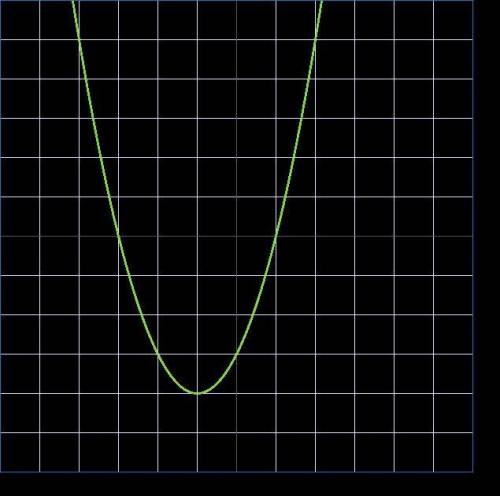
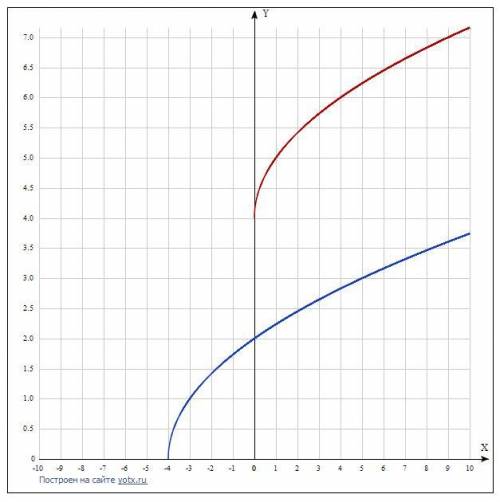
маєш в файлі синя- перша, червона -друга( побудуй функцію онлайн і перемалюй таблицю точок)
5. Область визначення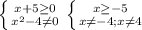
Відповідь: ОДЗ: х ∈ [-5;-4) ∪(-4;4) ∪(4;+∞).
6) хв=-4 ; -4=-p/2*1;p=8
ув=6
6=(-4)²+8(-4)+q;
q=6-16+32=22
f(x)=x²+8x+22
p=8 q=22
Алгоритм. Первым ходом Вася называет 1. Если число x оканчивается на k нулей, то S(x – 1) = 2011 + 9k. Таким образом Вася узнаёт положение самой правой ненулевой цифры в x. Положим x1 = x – 10k. Вася знает, что S(x1) = 2011. Подобрав на втором ходу число a так, что x – a = x1 – 1, Вася узнаёт сколько нулей в конце x1. Пусть их m. Положим x2 = x1 – 10m. Тогда S(x2) = 2010. Подобрав на третьем ходу число a так, что
x – a = x2 – 1, Вася узнаёт сколько нулей в конце x2, и т. д. После 2012 хода он получит S(x2012) = 0, тем самым найдя x.
Оценка. Пусть Петя признался, что в записи x есть только нули и единицы, то есть x = 10k2012 + 10k2011 + ... + 10k1, где k2012 > k2011 > ... > k1. При этом задача Васи сводится к выяснению значений показателей ki. Пусть Васе не везёт, и на i-м ходу оказывается, что 10ki больше предъявленного Васей числа a. Тогда, независимо от значений k2012, ..., ki+1, S(x – a) = S(10ki – a) + (2012 – i). Тем самым, о значениях k2012, ..., ki+1 ничего не известно (кроме того, что все они больше ki). В частности, после 2011 ходов может остаться неизвестным точное значение k2012.
ответ 2012ходов