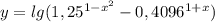
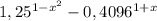было положительно, поскольку стоит в показателе логарифма, а показатель логарифма, будь то линейный, десятичный, в любом случае должен быть положителен: 
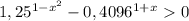, значит,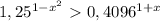 
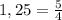— с этим, думаю, всё понятно и проблем не возникает, а вот второе число... внимательно смотрим на него и замечаем, что это точный квадрат числа 
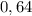, являющегося в то же время точным квадратом восьми десятых; получается, что 
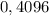— это 
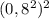, то есть 
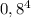или, вставшее по соседству с этим числом, 
. 
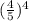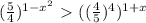
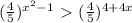
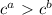может быть преобразовано в неравенство 
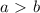при условии, что 
– константа, и что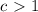 
; если 
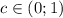, то неравенство 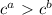принимает следующий вид: 
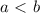; пользуясь им, переписываем наше неравенство в следующем виде: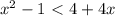 
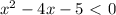
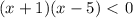
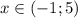
Решаем линейное неравенство 7x - 11 ≥ 10x - 8 для этого будем использовать тождественные преобразования, но при этом мы будем внимательно следить за знаком неравенства.
Перенесем в правую часть неравенства слагаемые без переменной, а в левую слагаемые содержащие переменную х.
При переносе слагаемых из одной части неравенства в другую меняем знак слагаемого на противоположный.
Знак неравенства при этом остается тем же:
7х - 10х ≥ - 8 + 11;
- 3х ≥ 3.
Разделим на - 3 обе части неравенства, при этом знак неравенства меняем на противоположный:
х ≤ - 1.
ответ: х принадлежит промежутку (- бесконечность; - 1]