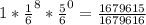б) меньше 8 раз выпала "четверка" из восьми бросков, от обратного, 1(полная вероятность) минус вероятность выпадения 8 раз подряд четверки. Туда войдут случае когда вообще ни разу четверка не выпадала.
Пусть число фотографий х. число пакетов у. 12*у+1=х мы записали условие Если положить в каждый пакет по 12 фотографий,то одна останется. (y-1)*k=x пакетов взять на один меньше,то все фотографии можно разложить поровну запишем систему 12y+1=x ky-k=x 12y+1=ky-k k+1=y(k-12) y=(k+1)/(k-12)=(1+13/(k-12)) k и целые числа и положительны и y>1 13/(k-12) lдолжно быть целым. но 13 простое число, значит знаменатель тоже равевен 13 или 1 k-12=1 k=13 k-12=13 k=25 y1=7 y2=2 x1=12*7+1= 85 x2=12*2+1=25 ответ число фотографий могло быть 25 или 85
Шанс выпадения p=1/6; невыпадения q=5/6;
В обоих случаях применим формулу Бернулли:
a) три раза выпала "четверка" из восьми бросков:
P³₈=C³₈p³q⁵=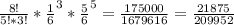
б) меньше 8 раз выпала "четверка" из восьми бросков, от обратного, 1(полная вероятность) минус вероятность выпадения 8 раз подряд четверки. Туда войдут случае когда вообще ни разу четверка не выпадала.
1-P⁸₈=C⁸₈p⁸q⁰=