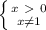
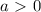Треугольник abc . ab - ? , на 5 см больше чем сторона ac. сторона bc- ? , на 5 см больше чем ab. p = 60 см. сильно надо!

👇

Увидеть ответ

Ответ:

savva137

26.01.2022

Х +[х+5]+[х+5+5]=60 3х+15=60. 3х=60-15. 3х=45. Х=45:3. Х=15. АС=15 АВ=20 ВС=25

4,6(62 оценок)

Открыть все ответы

Ответ:

ANNA040506

26.01.2022

Для начала замечу, что под знак корня входит и логарифм. Поэтому я обязан наложить следующие ограничения:
$\left \{ {{x \ \textgreater \ 0} \atop {x \neq 1}} \right.$
Кроме того, отсюда же следует ограничение и на параметр: $a \ \textgreater \ 0$ .

Теперь преобразую подкоренное выражение таким образом:
$\sqrt[10]{ a^{8} x^{0,25} - x^{0,25} x^{ log_{x} a^{x} } - a^{8 + 0,25} + a^{x} a^{0,25} } = \\ \sqrt[10]{ a^{8} x^{0,25} - x^{0.25} a^{x} - a^{8} a^{0,25} + a^{x} a^{0,25} } = \\ \sqrt[10]{(a^{8} x^{0,25} - x^{0.25} a^{x}) - (a^{8} a^{0,25} - a^{x} a^{0,25})} = \\ \sqrt[10]{ x^{0,25} (a^{8} - a^{x}) - a^{0,25}(a^{8} - a^{x})} = \\ \sqrt[10]{( a^{8} - a^{x} )( \sqrt[4]{x} - \sqrt[4]{a}) }$

Вспоминаем теперь о том, что корень чётной степени имеет смысл, если его подкоренное выражение неотрицательно, то есть, отсюда следует неравенство
$( a^{8} - a^{x} )( \sqrt[4]{x} - \sqrt[4]{a} ) \geq 0$
Для решения этого неравенства используем метод рационализации(все необходимые ограничения мы уже наложили ранее):

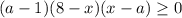
$(a - 1)(8 - x)(x - a) \geq 0$

Теперь необходимо исследовать полученное неравенство. Решаем его методом интервалов:

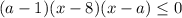
$(a - 1)(x - 8)(x - a) \leq 0$

Отсюда уже видим:
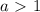1)Пусть $a \ \textgreater \ 1$ . Тогда
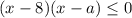
     $(x - 8)(x - a) \leq 0$
     Здесь возникают следующие подслучаи(в зависимости от расположения точек x = 8 и x = a на числовой оси):
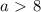
     а) $a \ \textgreater \ 8$

          Тогда неравенство решением имеет отрезок [8,a]

         Очевидно, условие x > 0 для данного отрезка выполняется(поскольку, очевидно, в этом случае x > 8) и икс отличен от 1(по такой же причине).
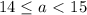         То есть, в этом случае область определения функции состоит только из указанного отрезка. Чтобы в неём лежало ровно 7 целых точек необходимо, чтобы $14 \leq a \ \textless \ 15$ . Правый конец не включаем, поскольку при a = 15 в области определения будет лежать и восьмая целая точка.

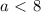       б)Пусть теперь $a \ \textless \ 8$ , а с учётом рассматриваемых а, 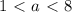$1 \ \textless \ a \ \textless \ 8$ . Тогда точка x = 8 лежит правее точки x = a и решение неравенства будет иметь вид: [a, 8]

.
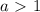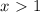Проверим выполнение остальных условий на данном отрезке. Поскольку $a \ \textgreater \ 1$ , то $x \ \textgreater \ 1$ заведомо. Оба ограничения здесь выполняются, а потому указанный отрезок и есть область определения нашей функции.
Очевидно, что ровно 7 точек на данном отрезке будут лишь, когда a ∈ (1,2]

. Правый конец обязан входить, а вот левый обязан не входить, поскольку иначе на отрезке будет 8 целых точек. Поскольку все эти значения больше 1, то эти интервалы пойдут в ответ.

в)Пусть теперь a = 8

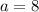. Тогда получаем неравенство
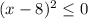             $(x-8)^{2} \leq 0$ , которое, очевидно, выполняется лишь в одной точке(x = 8). Значит, a = 8 условию задачи не удовлетворяет.

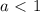2)Пусть $a \ \textless \ 1$ . Тогда 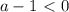$a -1 \ \textless \ 0$ и неравенство преобразуется так: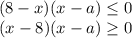

           $(8-x)(x-a) \leq 0 \\ (x-8)(x-a) \geq 0$
Ясно, что случай a < 1 нас не устраивает вообще, поскольку неравенство будет иметь своими решениями лишь бесконечные интервалы и обеспечить наличие ровно 7 точек в области определения функции точно не удастся.

3)Пусть a = 1

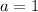. Тогда a - 1 = 0 и неравенство имеет вид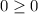
$0 \geq 0$
В этом случае неравенство выполняется ДЛЯ ЛЮБЫХ x. Ситуация та же самая. Обеспечить наличие в точности 7 точек в области определения мы не сможем.

Поэтому ответ задачи такой:

∈

∪

4,5(15 оценок)

Ответ:

romaantonizin

26.01.2022

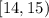
Из села А в село В, расстояние между которыми равно 140 км, выехал мотоциклист. За 20 минут до этого навстречу ему из B в A выехал велосипедист, который встретился с мотоциклистом через 2 часа после своего выезда. Найдите скорость каждого из них, если мотоциклист за 2 часа проезжает на 104 км больше, чем велосипедист за 4 часа.

Объяснение:

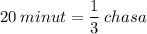
$20\: minut =\dfrac{1}{3} \: chasa$

$2-\dfrac{1}{3} =1\dfrac{2}{3} \text {(chasa) - vremya v puti motociklista do momenta vstrechi s velosipedistom.}$ Пусть х км/ч - скорость велосипедиста, тогда скорость мотоциклиста равна:

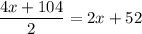
$\dfrac{4x+104}{2} =2x+52$

Скорость сближения мотоциклиста и велосипедиста равна:

x + 2x + 52 = 3x + 52 (км/ч)

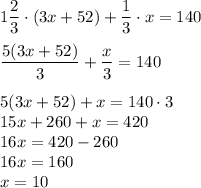
$1\dfrac{2}{3} \cdot (3x+52)+\dfrac{1}{3} \cdot x = 140\\\\\dfrac{5(3x+52)}{3}+\dfrac{x}{3} =140\\\\5(3x+52)+x=140 \cdot 3\\15x+260+x=420\\16x=420-260\\16x=160\\x=10$